题目内容
下列各组中的两个命题互为等价命题的是
- A.a∈A与a∈A∩B
- B.a∈A与a∈A∪B
- C.A∩B=A与A∪B=B
- D.a∈A∩B与a∈A∪B
C
分析:a∈A表示元素a是集合A的元素,a∈A∩B表示元素a是集合A和B的公共元素,a∈A∪B表示元素a是集合A或B的元素,A∩B=A表示A是B的子集,A∪B=B也表示A是B的子集,由此入手能够求出结果.
解答:∵a∈A表示元素a是集合A的元素,
a∈A∩B表示元素a是集合A和B的公共元素,
∴a∈A与a∈A∩B不是等价命题.
∵a∈A表示元素a是集合A的元素,
a∈A∪B表示元素a是集合A或B的元素,
∴a∈A与a∈A∪B不是等价命题.
∵A∩B=A表示A是B的子集,A∪B=B也表示A是B的子集,
∴A∩B=A与A∪B=B是等价命题.
∵a∈A∩B表示元素a是集合A和B的公共元素,
a∈A∪B表示元素a是集合A或B的元素,
∴a∈A∩B与a∈A∪B不是等价命题.
故选C.
点评:本题考查元素与集合、集合与集合间的相互关系,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
分析:a∈A表示元素a是集合A的元素,a∈A∩B表示元素a是集合A和B的公共元素,a∈A∪B表示元素a是集合A或B的元素,A∩B=A表示A是B的子集,A∪B=B也表示A是B的子集,由此入手能够求出结果.
解答:∵a∈A表示元素a是集合A的元素,
a∈A∩B表示元素a是集合A和B的公共元素,
∴a∈A与a∈A∩B不是等价命题.
∵a∈A表示元素a是集合A的元素,
a∈A∪B表示元素a是集合A或B的元素,
∴a∈A与a∈A∪B不是等价命题.
∵A∩B=A表示A是B的子集,A∪B=B也表示A是B的子集,
∴A∩B=A与A∪B=B是等价命题.
∵a∈A∩B表示元素a是集合A和B的公共元素,
a∈A∪B表示元素a是集合A或B的元素,
∴a∈A∩B与a∈A∪B不是等价命题.
故选C.
点评:本题考查元素与集合、集合与集合间的相互关系,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
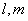 表示两条不同直线,
表示两条不同直线,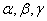 表示三个不同平面,条件:
表示三个不同平面,条件: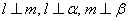 ; ②
; ②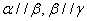 ;
③
;
③ ;
④
;
④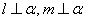 .
.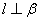 b:
b: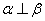 c:
c: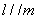 d:
d: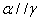 .
. b,
②
b,
②