题目内容
给定两个数列 ,
, 满足
满足 ,
, ,
,  .证明对于任意的自然数n,都存在自然数
.证明对于任意的自然数n,都存在自然数 ,使得
,使得 .
.
 ,
, 满足
满足 ,
, ,
,  .证明对于任意的自然数n,都存在自然数
.证明对于任意的自然数n,都存在自然数 ,使得
,使得 .
.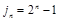
试题分析:先由
 得到数列
得到数列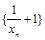 为等比数列,再求出
为等比数列,再求出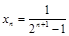 ;由
;由 得到
得到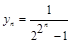 ,通过比较得到结果。
,通过比较得到结果。解:由已知得到:
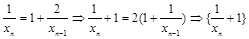 为等比数列,首项为2,公比为2,
为等比数列,首项为2,公比为2, 所以
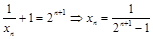 .
.又由已知,
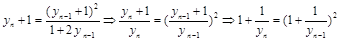
由
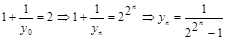 ,
, 所以取
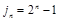 即可.
即可.点评:要求出一般数列的通项公式,常通过转化为等差数列或等比数列来得到。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
题目内容
 ,
, 满足
满足 ,
, ,
,  .证明对于任意的自然数n,都存在自然数
.证明对于任意的自然数n,都存在自然数 ,使得
,使得 .
.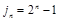
 得到数列
得到数列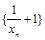 为等比数列,再求出
为等比数列,再求出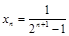 ;由
;由 得到
得到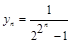 ,通过比较得到结果。
,通过比较得到结果。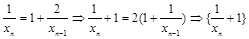 为等比数列,首项为2,公比为2,
为等比数列,首项为2,公比为2, 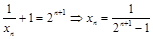 .
.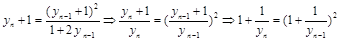
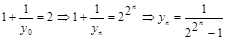 ,
, 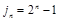 即可.
即可.
 计算高手系列答案
计算高手系列答案