Question

（2012•武昌区模拟）已知抛物线方程为y²=4x，直线l的方程为x-y+4=0，在抛物线上有一动点P到y轴的距离为d₁，P到直线l的距离为d₂，则d₁+d₂的最小值为（　　）

• A．

  5 2

  2

  +2
• B．

  5 2

  2

  +1
• C．

  5 2

  2

  -2
• D．

  5 2

  2

  -1

Answer 1

分析：如图点P到y轴的距离等于点P到焦点F的距离减1，过焦点F作直线x-y+4=0的垂线，此时d₁+d₂最小，根据抛物线方程求得F，进而利用点到直线的距离公式求得d₁+d₂的最小值．

解答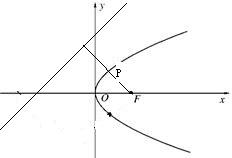：解：如图点P到准线的距离等于点P到焦点F的距离，
从而P到y轴的距离等于点P到焦点F的距离减1．
过焦点F作直线x-y+4=0的垂线，此时d₁+d₂=|PF|+d₂-1最小，
∵F（1，0），则|PF|+d₂=

|1-0+4|

1+1

=

5 2

2

，
则d₁+d₂的最小值为

5 2

2

-1．
故选D．

点评：本题主要考查了抛物线的简单性质，两点距离公式的应用．解此列题设和先画出图象，进而利用数形结合的思想解决问题．