Question

（2012•武昌区模拟）如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD，AB=

2

AD，E是线段PD上的点，F是线段AB上的点，且

PE

ED

=

BF

FA

=λ(λ＞0)．
（Ⅰ）当λ=1时，证明DF⊥平面PAC；
（Ⅱ）是否存在实数λ，使异面直线EF与CD所成的角为60°？若存在，试求出λ的值；若不存在，请说明理由．

Answer 1

分析：（Ⅰ）以A为坐标原点，建立空间直角坐标系，用坐标表示向量，证明

DF

•

AC

=0，

DF

•

AP

=0，即可证得DF⊥平面PAC；
（Ⅱ）设PA=AD=1，则AB=PD=

2

，确定

FE

=(-

2

1+λ

，

λ

1+λ

，

1

1+λ

)，

CD

=(-

2

，0，0)，利用向量的夹角公式，及异面直线EF与CD所成的角为60°，建立方程即可得到结论．

解答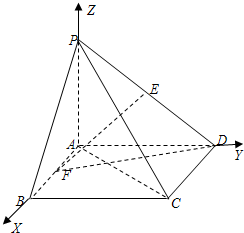：（Ⅰ）证明：以A为坐标原点，建立如图所示的空间直角坐标系．
当λ=1时，则F为AB的中点，设PA=AD=1，则AB=PD=

2

，则
A（0，0，0），C（

2

，1，0），P（0，0，1），D（0，1，0），F（

2

2

，0，0）．
∴

DF

=(

2

2

，-1，0)，

AC

=(

2

，1，0)，

AP

=（0，0，1）．
∴

DF

•

AC

=0，

DF

•

AP

=0，
∴

DF

⊥

AC

，

DF

⊥

AP

．
∵AC∩AP=A
∴DF⊥平面PAC；
（Ⅱ）解：设PA=AD=1，则AB=PD=

2

，则A（0，0，0），C（

2

，1，0），P（0，0，1），D（0，1，0），．
∵

PE

ED

=

BF

FA

=λ(λ＞0)，
∴F（

2

λ+1

，0，0），E（0，

λ

1+λ

，

1

1+λ

）．
∴

FE

=(-

2

1+λ

，

λ

1+λ

，

1

1+λ

)，

CD

=(-

2

，0，0)，∴

FE

•

CD

=

2

1+λ

．
依题意，有

1

2

=cos＜

FE

，

CD

＞=

FE • CD

| FE || CD |

，
∵λ＞0，∴

1

2

=

2

λ2+3

，∴λ=

5

．
∴存在实数λ=

5

，使异面直线EF与CD所成的角为60°．

点评：本题考查线面垂直，考查线线角，考查利用空间向量解决立体几何问题，关键是建立坐标系，用坐标表示点与向量．