题目内容
8.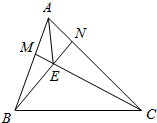 如图,在△ABC中,$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$,$\overrightarrow{AN}=\frac{1}{4}\overrightarrow{AC}$,BN与CM交于点E,若$\overrightarrow{AE}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x+y=$\frac{5}{11}$.
如图,在△ABC中,$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$,$\overrightarrow{AN}=\frac{1}{4}\overrightarrow{AC}$,BN与CM交于点E,若$\overrightarrow{AE}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x+y=$\frac{5}{11}$.
分析 可根据共线向量基本定理,由B,E,N三点共线得到$\overrightarrow{BE}=λ\overrightarrow{BN}$,进一步便得到$\overrightarrow{AE}=(1-λ)\overrightarrow{AB}+\frac{λ}{4}\overrightarrow{AC}$,而同理可由C,E,M三点共线得到$\overrightarrow{AE}=(1-μ)\overrightarrow{AC}+\frac{μ}{3}\overrightarrow{AB}$,从而便有$\left\{\begin{array}{l}{1+λ=\frac{μ}{3}}\\{\frac{λ}{4}=1-μ}\end{array}\right.$,这样解出λ,μ便可用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AE}$,从而求出x+y.
解答 解:B,E,N三点共线;
∴$\overrightarrow{BE}=λ\overrightarrow{BN}$;
∴$\overrightarrow{AE}-\overrightarrow{AB}=λ(\overrightarrow{AN}-\overrightarrow{AB})$;
∴$\overrightarrow{AE}=(1-λ)\overrightarrow{AB}+\frac{λ}{4}\overrightarrow{AC}$①;
同理由C,E,M三点共线可得:$\overrightarrow{AE}=(1-μ)\overrightarrow{AC}+\frac{μ}{3}\overrightarrow{AB}$②;
∴由①②得,$\left\{\begin{array}{l}{1-λ=\frac{μ}{3}}\\{\frac{λ}{4}=1-μ}\end{array}\right.$;
解得$λ=\frac{8}{11},μ=\frac{9}{11}$;
∴$\overrightarrow{AE}=\frac{3}{11}\overrightarrow{AB}+\frac{2}{11}\overrightarrow{AC}$;
又$\overrightarrow{AE}=x\overrightarrow{AB}+y\overrightarrow{AC}$;
∴$x+y=\frac{5}{11}$.
故答案为:$\frac{5}{11}$.
点评 考查共线向量基本定理,平面向量基本定理,以及的加法、减法,及数乘运算,向量减法的几何意义.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案| A. | $y={log_{\frac{1}{2}}}(x+1)$ | B. | $y={log_2}\sqrt{{x^2}-1}$ | C. | $y={log_2}\frac{1}{x}$ | D. | $y={log_{0.2}}(4-{x^2})$ |
| A. | f(x)=1与g(x)=x0 | B. | $f(x)=\root{3}{x^3}$与g(x)=x | C. | f(x)=x与$g(x)={(\sqrt{x})^2}$ | D. | f(x)=x与$g(x)=\sqrt{x^2}$ |