题目内容
已知函数y=
x-
的图象为中心是坐标原点O的双曲线,在此双曲线的两支上分别取点P,Q,则线段PQ的最小值为
| 3 |
| 1 |
| x |
2
-2
| 3 |
2
-2
.| 3 |
分析:先找出两条渐近线,一条为x=0,一条为y=
x,由此可知此双曲线的对称轴方程,求出此对称轴与双曲线的交点,即可求出最小距离.
| 3 |
解答: 解:函数y=
解:函数y=
x-
的导数为y′=
+
>
,所以函数的渐近线方程为:x=0与y=
x,
两条渐近线的角的平分线与x轴所成的倾斜角为-15°,其方程为:y=tan(-15°)x=(
-2)x,
它与函数y=
x-
的交点为:(
,-
),(-
,
),
PQ两点的最短距离为:2
-2.
故答案为:2
-2.
 解:函数y=
解:函数y=| 3 |
| 1 |
| x |
| 3 |
| 1 |
| x2 |
| 3 |
| 3 |
两条渐近线的角的平分线与x轴所成的倾斜角为-15°,其方程为:y=tan(-15°)x=(
| 3 |
它与函数y=
| 3 |
| 1 |
| x |
| ||
| 2 |
| ||||
| 2 |
| ||
| 2 |
| ||||
| 2 |
PQ两点的最短距离为:2
| 3 |
故答案为:2
| 3 |
点评:本题考查双曲线的基本性质,利用函数的导数求出函数的斜率范围,推出双曲线的渐近线,求出双曲线的对称轴方程是解题的关键.

练习册系列答案
相关题目
已知函数y=3x-4的值域为[-10,5],则它的定义域是( )
| A、[-2,3] | B、[-1,4] | C、[-2,2] | D、[-1,3] |
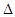 x=0.1,则
x=0.1,则