题目内容
【题目】如图，四棱锥
的底面是正方形，
底面ABCD，点E在棱PB上．
求证：平面
平面PDB；
当
，且E为PB的中点时，求AE与平面PDB所成的角的大小．
【答案】（1）见解析；（2）
【解析】
1
欲证平面
平面PDB，根据面面垂直的判定定理可知在平面AEC内一直线与平面PDB垂直，而根据题意可得
平面PDB；2设
，连接OE，根据线面所成角的定义可知
为AE与平面PDB所的角，在
中求出此角即可．
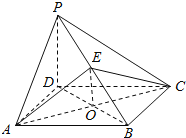
1证明：
四边形ABCD是正方形，
，
底面ABCD，
，
平面PDB，
平面平面PDB．
2解：设，连接OE，
由Ⅰ知平面PDB于O，
为AE与平面PDB所的角，
，E分别为DB、PB的中点，
，
，
又底面ABCD，
底面ABCD，
，
在中，
，
，即AE与平面PDB所成的角的大小为．
练习册系列答案
相关题目
【题目】为弘扬“中华优秀传统文化”，某中学在校内对全体学生进行了一次检测，规定分数
分为优秀，为了解学生的测试情况，现从2000名学生中随机抽取100名学生进行分析，按成绩分组，得到如下频数分布表。
分数 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
频数 | 5 | 35 | 30 | 20 | 10 |
（1）在图中作出这些数据的频率分布直方图；
（2）估计这次测试的平均分；
（3）估计这次测试成绩的中位数。
