题目内容
8.函数函数y=${3}^{{x}^{2}-2x}$的单调递增区间为( )| A. | (-∞,1) | B. | (-∞,-1) | C. | (1,+∞) | D. | (3,+∞) |
分析 可以看出原函数是由y=3t和t=x2-2x复合而成的复合函数,y=3t为增函数,从而t=x2-2x的增区间便是原函数的增区间,从而求二次函数t=x2-2x的增区间即可.
解答 解:令x2-2x=t,y=3t为增函数;
∴t=x2-2x的单调递增区间为原函数的单调增区间;
∴原函数的单调递增区间为(1,+∞).
故选:C.
点评 考查复合函数的单调性,以及指数函数、二次函数的单调性,清楚复合函数是由哪两个函数复合而成的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知集合全集U=R,M={x|x<1},N={x|log2x<1},则M∩(∁UN)=( )
| A. | ∅ | B. | {x|x≤0} | C. | {x|x<1} | D. | {x|x≥2} |
16.函数f(x)=-x3-3x2-3x的单调减区间为( )
| A. | (0,+∞) | B. | (-∞,-1) | C. | (-∞,+∞) | D. | (-1,+∞) |
18.若f(x)是偶函数,g(x)是奇函数,它们由相同的定义域,且f(x)+g(x)=$\frac{1}{x-1}$.则( )
| A. | f(x)=$\frac{2}{{x}^{2}-1}$ | B. | f(x)=$\frac{1}{{x}^{2}-1}$ | C. | f(x)=$\frac{2x}{{x}^{2}-1}$ | D. | f(x)=$\frac{x}{{x}^{2}-1}$ |
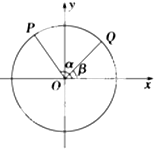 如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于P,Q两点,已知点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$
如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于P,Q两点,已知点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$