Question

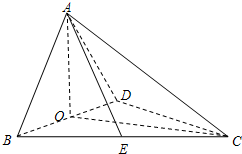（2013•崇明县一模）如图，四面体ABCD中，O、E分别是BD、BC的中点，AO⊥平面BCD，CA=CB=CD=BD=2．
（1）求三棱锥A-BCD的体积；
（2）求异面直线AE与CD所成角的大小．

Answer 1

分析：（1）利用等边三角形的性质、线面垂直的性质定理、勾股定理、三棱锥的体积计算公式即可得出；
（2）利用三角形的中位线定理、异面直线所成的角、线面垂直的性质定理即可求出．

解答：解：（1）在等边三角形△BCD中，BO=OD=1，∴CO=

3

．
∵AO⊥平面BCD，∴AO⊥OC．
在Rt△AOC中，由勾股定理得OA=

22-( 3 )2

=1．
∴VA-BCD=

1

3

S△BCD×OA=

1

3

×

3

4

×22×1=

3

3

．
（2）连接OE，∵O、E为中点，∴OE∥CD，OE=

1

2

CD=1，∴∠AEO或其补角为异面直线AE与CD所成角．
∵AO⊥平面BCD，∴AO⊥OE．
在直角三角形AEO中，∵OA=OE，
∴∠AEO=

π

4

，所以异面直线AE与CD所成角的大小为

π

4

．

点评：熟练掌握等边三角形的性质、线面垂直的性质定理、勾股定理、三棱锥的体积计算公式、三角形的中位线定理、异面直线所成的角是解题的关键．