题目内容

请考生在第22，23，24题中任选一题作答，如果多做，则按所做的第一题记分．作答时请写清题号．
如图，∠BAC的平分线与BC和外接圆分别相交于D和E，延长AC交过D，E，C三点的圆于点F．
（Ⅰ）求证：EF2=ED•EA；
（Ⅱ）若AE=6，EF=3，求AF•AC的值．
分析：（Ⅰ）连接CE，DF，由AE平分∠BAC，知∠BAD=∠DAC，在圆内由∠DCE=∠EFD，∠BCE=∠BAE，知∠EAF=∠EFD，导出△AEF∽△FED，由此能够证明EF2=ED•EA．
（Ⅱ）由EF2=ED•EA，EF=3，AE=6，知ED=
3
2
，AD=
9
2
，由此能求出AF•AC的值．
解答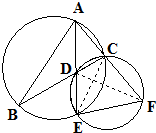：（Ⅰ）证明：如图，连接CE，DF，
∵AE平分∠BAC，
∴∠BAD=∠DAC，
在圆内又知∠DCE=∠EFD，∠BCE=∠BAE，
∴∠EAF=∠EFD，
又∠AEF=∠FED，
∴△AEF∽△FED，∴
EF
ED
=
AE
EF
，
∴EF2=ED•EA．…（5分）
（Ⅱ）解：由（Ⅰ）知EF2=ED•EA，
∵EF=3，AE=6，
∴ED=
3
2
，AD=
9
2
，
∴AC•AF=AD•AE=6×
9
2
=27．…（10分）
点评：本题考查与圆有关的比例线段的应用，解题时要认真审题，仔细解答，注意三角形相似的灵活运用．
练习册系列答案
相关题目
已知定义在（0，+∞）上的三个函数f（x）=lnx，g（x）=x2-af（x），h(x)=x-a
x
，且g（x）在x=1处取得极值．
（Ⅰ）求函数g（x）在x=2处的切线方程；
（Ⅱ）求函数h（x）的单调区间；
（Ⅲ）把h（x）对应的曲线C1向上平移6个单位后得到曲线C2，求C2与g（x）对应曲线C3的交点个数，并说明理由．
请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题记分．
作答时，用2B铅笔在答题卡上把所选题目对应的题号涂黑．
（2012•太原模拟）设函数f(x)=a(x+
1
x
)+2lnx，g(x)=x2．
（1）若a=
1
2
时，直线l与函数f（x）和函数g（x）的图象相切于同一点，求切线l的方程；
（2）若f（x）在[2，4]内为单调函数，求实数a的取值范围．
说明：请考生在第22、23、24三题中任选一题作答，如果多做，则按所做第一题记分．

（请考生在第22、23两题中任选一题作答，如果多做。则按所做的第一题记分．
（本小题满分10分）选修4－1：几何证明选讲
如图：AB是⊙O的直径，G是AB延长线上的一点，GCD是⊙O的割线，过点G作AG的垂线，交直线AC于点E，交直线AD于点F，过点G作⊙O的切线，切点为H．求证：

（Ⅰ）C、D、F、E四点共圆；
（Ⅱ）GH2＝GE·GF．

选做题：请考生在第22，23，24题中任选一题做答，如果多做，则按所做的第一题记分

22．（本小题满分10分）选修4—1几何证明选讲

如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于点D，DE⊥AC，交AC的延长线于点E，OE交AD于点F。

   （I）求证：DE是⊙O的切线；

   （II）若的值.

 

23．（本小题满分10分）选修4—2坐标系与参数方程

        设直角坐标系原点与极坐标极点重合， x轴正半轴与极轴重合，若已知曲线C的极坐标方程为，点F1、F2为其左、右焦点，直线l的参数方程为

   （I）求直线l的普通方程和曲线C的直角坐标方程；

   （II）求曲线C上的动点P到直线l的最大距离。

24．（本小题满分10分）选修4—5不等式选讲

        对于任意的实数恒成立，记实数M的最大值是m。

   （1）求m的值；

   （2）解不等式

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网