题目内容
【题目】函数f（x）=|x|﹣ 
（a∈R）的图象不可能是（ ）
A.
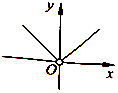
B.
C.
D.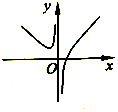
【答案】C
【解析】解：f（x）=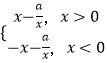 
，∴f′（x）= 
．（1）当a=0时，f（x）= 
，图象为A；（2）当a＞0时，1+ 
＞0，∴f（x）在（0，+∞）上单调递增，
令﹣1+ =0得x=﹣ 
，∴当x＜﹣ 时，﹣1+ ＜0，当﹣ ＜x＜0时，﹣1+ ＞0，
∴f（x）在（﹣∞，﹣ ）上单调递减，在（﹣ ，0）上单调递增，图象为D；（3）当a＜0时，﹣1+ ＜0，∴f（x）在（﹣∞，0）上单调递减，
令1+ =0得x= 
，∴当x＞ 时，1+ ＞0，当0＜x＜ 时，1+ ＜0，
∴f（x）在（0， ）上单调递减，在（ ，+∞）上单调递增，图象为B；
故选C．
【考点精析】本题主要考查了函数的图象的相关知识点，需要掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值才能正确解答此题．
练习册系列答案
综合自测系列答案
相关题目
【题目】某经销商从外地水产养殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如图：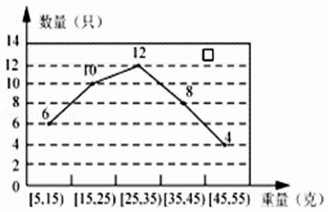 
（1）记事件A为：“从这批小龙虾中任取一只，重量不超过35g的小龙虾”，求P（A）的估计值；
（2）若购进这批小龙虾100千克，试估计这批小龙虾的数量；
（3）为适应市场需求，了解这批小龙虾的口感，该经销商将这40只小龙虾分成三个等级，如下表：
等级 | 一等品 | 二等品 | 三等品 |
重量（g） | [5，25） | [25，45） | [45，55] |
按分层抽样抽取10只，再随机抽取3只品尝，记X为抽到二等品的数量，求抽到二级品的期望．
