题目内容
【题目】已知函数f（x）=lnx﹣ax（a＞0），设 
．
（1）判断函数h（x）=f（x）﹣g（x）零点的个数，并给出证明；
（2）首项为m的数列{an}满足：①an+1+an≠ 
；②f（an+1）=g（an）．其中0＜m＜ 
．求证：对于任意的i，j∈N* ， 均有ai﹣aj＜ 
﹣m．
【答案】
（1）解：函数h（x）=f（x）﹣g（x）在 
上有且仅有一个零点．
证明如下：函数f（x）=lnx﹣ax的定义域为（0，+∞），
由 
，可得函数g（x）的定义域为（﹣∞， 
），
∴函数h（x）=f（x）﹣g（x）的定义域为（0， ）．
h（x）=f（x）﹣g（x）=lnx﹣ax﹣ln（ 
）+2﹣ax．
h′（x）=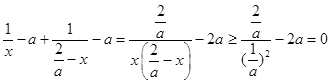 
，
当且仅当 
时等号成立，因此h（x）在 上单调递增，又 
，
故函数h（x）=f（x）﹣g（x）在 上有且仅有一个零点；
（2）证明：由（1）可知h（x）在 上单调递增，且 
，
故当 
时，h（x）＜0，即f（x）＜g（x）；
当 
时，h（x）＞0，即f（x）＞g（x）．
∵ 
，∴f（a1）＜g（a1）=f（a2），
若 
，则由 
，且f（x）在 
上单调递减，
知 
，即 
，这与 
矛盾，故 
，
而当 时，f（x）单调递增，故 
；
同理可证 
，…， 
，
故数列{an}为单调递增数列且所有项均小于 
，
因此对于任意的i，j∈N*，均有 
．
【解析】（1）由已知求出函数函数h（x）=f（x）﹣g（x）的定义域为（0， 
）．利用导数判断函数在定义域上是单调函数，再由 
可得函数h（x）=f（x）﹣g（x）在 
上有且仅有一个零点；（2）由（1）可知h（x）在 上单调递增，且 
，故当 
时，h（x）＜0，即f（x）＜g（x）；当 
时，h（x）＞0，即f（x）＞g（x）．由a1=m及m的范围可得f（a1）＜g（a1）=f（a2），然后判断得 
，结合 时，f（x）单调递增得 
；同理可证 
，…， 
，则有数列{an}为单调递增数列且所有项均小于 
，从而证得对于任意的i，j∈N*，均有 
．
