Question

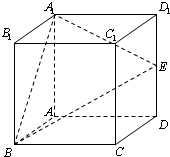如图所示，在正方体ABCD-A₁B₁C₁D₁中，E是棱DD₁的中点，F是侧面CDD₁C₁上的动点，且B₁F∥面A₁BE，则B₁F与平面CDD₁C₁ 所成角的正切值构成的集合是（　　）

• A、2
• B、{

  2

  5

  5

  }
• C、{t|2≤t≤2

  2

  }
• D、{t|

  2

  5

  5

  ≤t≤2}

Answer 1

分析：设G，H，I分别为CD、CC₁、C₁D₁边上的中点，根据面面平行的判定定理，可得平面A₁BGE∥平面B₁HI，结合已知中B₁F∥面A₁BE，可得F落在线段HI上，∠B₁FC₁即为B₁F与平面CDD₁C₁ 所成角，求出该角正切的最大值与最小值，即可得到答案．

解答：解：设G，H，I分别为CD、CC₁、C₁D₁边上的中点
则ABEG四点共面，
且平面A₁BGE∥平面B₁HI
又∵B₁F∥面A₁BE，
∴F落在线段HI上，
设HI的中点为J
则当F与J重合时，B₁F与平面CDD₁C₁ 所成角的正切值有最大值2

2

当F与H或I重合时，B₁F与平面CDD₁C₁ 所成角的正切值有最小值2
故B₁F与平面CDD₁C₁ 所成角的正切值构成的集合是{t|2≤t≤2

2

}
故选C．

点评：本题考查的知识点是直线与平面所成的角，其中分析出F落在线段HI上，是解答本题的关键．