题目内容
函数y=
的值的符号为（ ）
| sinα+tanα |
| cosα+cotα |
分析：将所求式子的分子与分母相乘，利用同角三角函数间的基本关系化简，约分后根据正弦及余弦函数的值域，确定出即的符合为正，得到两因式为同号，利用同号两数相除商为正，得到所求式子的值符合为正．
解答：解：∵sinα＞-1，cosα＞-1，
∴（sinα+tanα）（cosα+cotα）
=（sinα+
）（cosα+
）
=
•
=（cosα+1）（sinα+1）＞0，
∴sinα+tanα与cosα+cotα同号，
则y=
的值的符合为正．
故选A
∴（sinα+tanα）（cosα+cotα）
=（sinα+
| sinα |
| cosα |
| cosα |
| sinα |
=
| sinαcosα+sinα |
| cosα |
| sinαcosα+cosα |
| sinα |
=（cosα+1）（sinα+1）＞0，
∴sinα+tanα与cosα+cotα同号，
则y=
| sina+tana |
| cosa+cota |
故选A
点评：此题考查了同角三角函数间的基本关系，以及三角函数值的符合，熟练掌握基本关系是解本题的关键．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
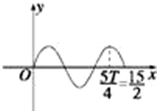已知函数y=sin| πx |
| 3 |
| A、6 | B、7 | C、8 | D、9 |