题目内容
(12分)经过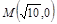 作直线
作直线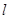 交曲线
交曲线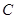 :
: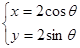 (
( 为参数)于
为参数)于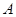 、
、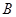 两点,若
两点,若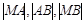 成等比数列,求直线
成等比数列,求直线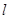 的方程.
的方程.

解析试题分析:把曲线的参数方程化为普通方程,由|AB|2=|MA|•|MB|,可得|AB|等于圆的切线长,设出直线l的方程,求出弦心距d,再利用弦长公式求得|AB|,由此求得直线的斜率k的值,即可求得直线l的方程.
解:直线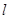 的参数方程:
的参数方程: (
( 为参数),…………①
为参数),…………①
曲线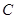 :
: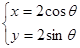 化为普通方程为
化为普通方程为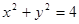 ,…………②
,…………②
将①代入②整理得: ,设
,设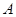 、
、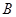 对应的参数分别为
对应的参数分别为 ,
,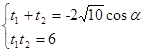 ,由
,由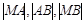 成等比数列得:
成等比数列得: ,
,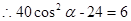 ,
,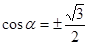 ,
, ,
,
直线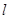 的方程为:
的方程为:
考点:本题主要考查把参数方程化为普通方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,属于基础题.
点评:解决该试题的关键是把曲线的参数方程化为普通方程,由|AB|2=|MA|•|MB|,可得|AB|等于圆的切线长,利用切割线定理得到,并结合勾股定理得到结论。

练习册系列答案
相关题目
数列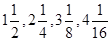 ,…前n项的和为
,…前n项的和为
A.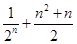 | B.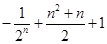 |
C.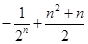 | D.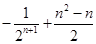 |
已知数列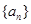 的通项公式为
的通项公式为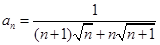
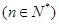 ,其前n项和为
,其前n项和为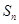 ,则在数列
,则在数列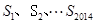 中,有理数项的项数为( )
中,有理数项的项数为( )
| A.42 | B.43 | C.44 | D.45 |
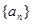 是等比数列,且
是等比数列,且 ,
,
 ,求
,求 的前
的前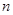 项的和
项的和
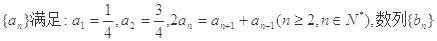 满足:
满足: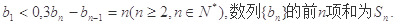
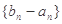 为等比数列;
为等比数列;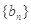 为递增数列;
为递增数列; 的取值范围。
的取值范围。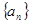 中,
中,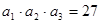 ,
,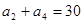
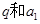 (2)求出
(2)求出
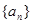 的公差
的公差 ,设
,设 ,
,
 ,求数列
,求数列 ,且
,且 成等比数列,求
成等比数列,求 的值;
的值;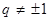 ,证明:
,证明: .
. 满足
满足 ,且
,且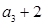 是
是 ,
,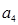 的等差中项.
的等差中项.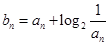 ,
,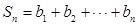 ,求使
,求使 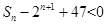 成立的
成立的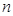 的最小值.
的最小值.  的前n项和记为
的前n项和记为 ,已知
,已知 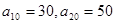 .
. ;
;