题目内容
(08年巢湖市质检二理) (13分)已知点R(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上 ,且满足![]() ,
,![]() .
.
(Ⅰ)⑴当点P在y轴上移动时,求点M的轨迹C的方程;
(Ⅱ)设![]() 为轨迹C上两点,且
为轨迹C上两点,且![]() ,N(1,0),求实数
,N(1,0),求实数![]() ,使
,使![]() ,且
,且![]() .
.
解析:(Ⅰ)设点M(x,y),由![]() 得P(0,
得P(0,![]() ),Q(
),Q(![]() ).
).
由![]() 得(3,
得(3,![]() )?(
)?(![]() ,
,![]() )=0,即
)=0,即![]()
又点Q在x轴的正半轴上,![]() 故点M的轨迹C的方程是
故点M的轨迹C的方程是![]() .……6分
.……6分
(Ⅱ)解法一:由题意可知N为抛物线C:y2=4x的焦点,且A、B为过焦点N的直线与抛物线C的两个交点。
当直线AB斜率不存在时,得A(1,2),B(1,-2),|AB|![]() ,不合题意;………7分
,不合题意;………7分
当直线AB斜率存在且不为0时,设![]() ,代入
,代入![]() 得
得![]()
则|AB|![]() ,解得
,解得![]() …………………10分
…………………10分
代入原方程得![]() ,由于
,由于![]() ,所以
,所以![]() ,
,
由![]() ,得
,得  . ……………………13分
. ……………………13分
解法二:由题设条件得
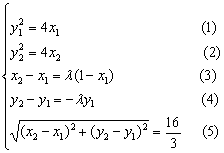

由(6)、(7)解得![]() 或
或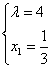 ,又
,又![]() ,故
,故![]() . …………………13分
. …………………13分

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目