题目内容
已知椭圆x2+| y2 |
| b2 |
(1)若椭圆的离心率e=
| ||
| 2 |
(2)若⊙P的圆心在直线x+y=0上,求椭圆的方程.
分析:(1)根据椭圆的离心率和长半轴求得半焦距c,进而求得b,进而可求得B,F,C的坐标,设出圆P的方程,把三点坐标代入后联立求得m,n和r,则所求圆的方程可得.
(2))根据⊙P过点F,B,C三点,可推断出圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,进而根据题意表示出FC和BC的垂直平分线方程联立后求得交点即圆心的坐标表达式,代入直线方程x+y=0求得b,则椭圆的方程可得.
(2))根据⊙P过点F,B,C三点,可推断出圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,进而根据题意表示出FC和BC的垂直平分线方程联立后求得交点即圆心的坐标表达式,代入直线方程x+y=0求得b,则椭圆的方程可得.
解答: 解:(1)当e=
解:(1)当e=
时,∵a=1,∴c=
,
∴b2=a2-c2=1-
=
,b=
,
点B(0,
),F(-
,0),C(1,0)
设⊙P的方程为(x-m)2+(y-n)2=r2,
由⊙P过点F,B,C得
∴m2+(
-n)2=r2①(m+
)2+n2=r2②(1-m)2+n2=r2③
由①②③联立解得:m=
,n=
,r2=
-
∴所求的⊙P的方程为(x-
)2+(y-
)2=
(2)∵⊙P过点F,B,C三点,
∴圆心P既在FC的垂直平分线上,
也在BC的垂直平分线上,FC的垂直平分线方程为x=
④
∵BC的中点为(
,
),kBC=-b
∴BC的垂直平分线方程为y-
=
(x-
)⑤
由④⑤得x=
,y=
,即m=
,n=
(
∵P(m,n)在直线x+y=0上,∴
+
=0?(1+b)(b-c)=0
∵1+b>0∴b=c,由b2=1-c2得b2=
∴椭圆的方程为x2+2y2=1
 解:(1)当e=
解:(1)当e=
| ||
| 2 |
| ||
| 2 |
∴b2=a2-c2=1-
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
点B(0,
| 1 |
| 2 |
| ||
| 2 |
设⊙P的方程为(x-m)2+(y-n)2=r2,
由⊙P过点F,B,C得
∴m2+(
| 1 |
| 2 |
| ||
| 2 |
由①②③联立解得:m=
2-
| ||
| 4 |
1-2
| ||
| 4 |
| 5 |
| 4 |
∴所求的⊙P的方程为(x-
2-
| ||
| 4 |
1-2
| ||
| 4 |
| 5 |
| 4 |
(2)∵⊙P过点F,B,C三点,
∴圆心P既在FC的垂直平分线上,
也在BC的垂直平分线上,FC的垂直平分线方程为x=
| 1-c |
| 2 |
∵BC的中点为(
| 1 |
| 2 |
| b |
| 2 |
∴BC的垂直平分线方程为y-
| b |
| 2 |
| 1 |
| b |
| 1 |
| 2 |
由④⑤得x=
| 1-c |
| 2 |
| b2-c |
| 2b |
| 1-c |
| 2 |
| b2-c |
| 2b |
∵P(m,n)在直线x+y=0上,∴
| 1-c |
| 2 |
| b2-c |
| 2b |
∵1+b>0∴b=c,由b2=1-c2得b2=
| 1 |
| 2 |
∴椭圆的方程为x2+2y2=1
点评:本题主要考查了椭圆的基本性质,椭圆与圆和直线的位置关系.考查了学生综合运用基础知识的能力和分析推理的能力.属中档题.

练习册系列答案
相关题目
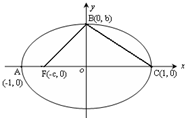 已知椭圆
已知椭圆