题目内容
已知椭圆x2+| y2 | b2 |
(1)当m+n>0时,求椭圆离心率的范围;
(2)直线AB与⊙P能否相切?证明你的结论.
分析:(1)先求F、B、C的坐标,求直线FC、BC的中垂线方程,解出P的坐标,m+n>0,得到a、b、c关系,求出e的范围.
(2)直线AB与⊙P能相切,则切点为B,求出AB和PB的斜率,如果垂直,斜率之积为-1,判断即可.
(2)直线AB与⊙P能相切,则切点为B,求出AB和PB的斜率,如果垂直,斜率之积为-1,判断即可.
解答:解:(1)设F、B、C的坐标分别为(-c,0),(0,b),(1,0),则FC、BC的中垂线分别为 x=
,
y-
=
(x-
).联列方程组,
解出
∴m+n=
+
>0,
即b-bc+b2-c>0,即(1+b)(b-c)>0,
∴b>c.
从而b2>c2即有a2>2c2,
∴e2<
.又 e>0,
∴0<e<
.
(2)直线AB与⊙P不能相切.由kAB=b,kPB=
=
.
如果直线AB与⊙P相切,则 b•
=-1.b2+c2=1
解出c=0或2,与0<c<1矛盾,
所以直线AB与⊙P不能相切.
| 1-c |
| 2 |
y-
| b |
| 2 |
| 1 |
| b |
| 1 |
| 2 |
解出
|
∴m+n=
| 1-c |
| 2 |
| b2-c |
| 2b |
即b-bc+b2-c>0,即(1+b)(b-c)>0,
∴b>c.
从而b2>c2即有a2>2c2,
∴e2<
| 1 |
| 2 |
∴0<e<
| ||
| 2 |
(2)直线AB与⊙P不能相切.由kAB=b,kPB=
b-
| ||
0-
|
| b2+c |
| b(c-1) |
如果直线AB与⊙P相切,则 b•
| b2+c |
| b(c-1) |
解出c=0或2,与0<c<1矛盾,
所以直线AB与⊙P不能相切.
点评:本题考查椭圆的性质,直线与圆的位置关系等知识,难度较大,容易出错.

练习册系列答案
相关题目
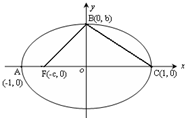 已知椭圆
已知椭圆