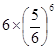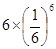题目内容
(3分)(2011•重庆)(1+3x)n(其中n∈N且n≥6)的展开式中x5与x6的系数相等,则n=( )
| A.6 | B.7 | C.8 | D.9 |
B
解析试题分析:利用二项展开式的通项公式求出二项展开式的通项,求出展开式中x5与x6的系数,列出方程求出n.
解:二项式展开式的通项为Tr+1=3rCnrxr
∴展开式中x5与x6的系数分别是35Cn5,36Cn6
∴35Cn5=36Cn6
解得n=7
故选B
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
设函数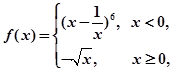 则当
则当 时,
时, 表达式的展开式中常数项为( )
表达式的展开式中常数项为( )
A. | B. | C. | D.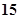 |
六个人从左至右排成一行,最左端只能排甲或乙,学科网最右端不能排甲,则不同的排法共有( )
A.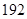 种 种 | B.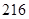 种 种 | C.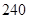 种 种 | D.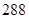 种 种 |
已知{1,2}⊆Z⊆{1, 2,3,4,5},满足这个关系式的集合Z共有 ( ).
| A.2个 | B.6个 | C.4个 | D.8个 |
从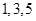 中选
中选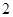 个不同数字,从
个不同数字,从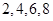 中选
中选 个不同数字排成一个五位数,则这些五位数中偶数的个数为( )
个不同数字排成一个五位数,则这些五位数中偶数的个数为( )
A.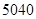 | B.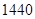 | C.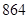 | D.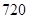 |
 的展开式中各项系数的和为2,则该展开式中常数项为( )
的展开式中各项系数的和为2,则该展开式中常数项为( )
| A.-40 | B.-20 | C.20 | D.40 |
某老师推荐甲、乙、丙、丁、戊5名同学到美术、音乐、舞蹈、速算四个兴趣班学习,每名同学只推荐一个兴趣班,每个兴趣班至少推荐一名学生,则不推荐甲同学到美术兴趣班的推荐方案有( )
| A.36种 | B.120种 | C.144种 | D.180种 |
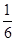 ,则李先生在一次上班途中会遇到堵车次数
,则李先生在一次上班途中会遇到堵车次数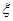 的期望值
的期望值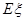 是( )
是( )