题目内容
下列命题:其中真命题的个数为
①若
=
+
,则P、A、B三点共线;
②已知
=(3,4),
=(-2,-1),则
在
上的投影为-2;
③在△ABC中,“
•
+
2=0”是“△ABC为直角三角形”的充要条件;
④△ABC的面积S△ABC=
•
•tanA.
0
0
.①若
| OP |
| 1 |
| 2 |
| OA |
| 1 |
| 3 |
| OB |
②已知
| AB |
| CD |
| AB |
| CD |
③在△ABC中,“
| AB |
| BC |
| AB |
④△ABC的面积S△ABC=
| 1 |
| 2 |
| AB |
| AC |
分析:①根据三点共线的条件判断.②根据向量的投影的概念判断.③根据数量积的应用判断.④根据三角形的面积公式进行判断.
解答:解:①若
=
+
,∵
+
≠1,∴P、A、B三点不共线,∴①错误.
②已知
=(3,4),
=(-2,-1),则
在
上的投影为
=
=
=-2
,∴②错误.
③在△ABC中,若
•
+
2=0,则|
||
|cos(π-B)+|
|2=0,即|
|cosB=|
|,“△ABC不一定是直角三角形,∴③错误.
④当三角形为直角三角形且A=90°时,三角形的面积公式S△ABC=
•
•tanA不成立,∴④错误.
故真命题的个数为0.
故答案为:0.
| OP |
| 1 |
| 2 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 2 |
| 1 |
| 3 |
②已知
| AB |
| CD |
| AB |
| CD |
| ||||
|
|
| -2×3+(-1)×4 | ||
|
| -10 | ||
|
| 5 |
③在△ABC中,若
| AB |
| BC |
| AB |
| AB |
| BC |
| AB |
| BC |
| AB |
④当三角形为直角三角形且A=90°时,三角形的面积公式S△ABC=
| 1 |
| 2 |
| AB |
| AC |
故真命题的个数为0.
故答案为:0.
点评:本题主要考查与平面向量有关 的命题的真假判断,要求熟练掌握平面向量的基本应用.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 >
>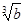 >0”的逆否命题
>0”的逆否命题