[题目]在等比数列{an}中.a2=3.a5=81． (Ⅰ)求an,(Ⅱ)设bn=log3an . 求数列{bn}的前n项和Sn ．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】在等比数列{an}中，a2=3，a5=81．（Ⅰ）求an；
（Ⅱ）设bn=log3an ，求数列{bn}的前n项和Sn ．

【答案】解：（Ⅰ）设等比数列{an}的公比为q，由a2=3，a5=81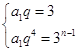，得
，解得．
∴ ；
（Ⅱ）∵ ，bn=log3an ，
∴ ．
则数列{bn}的首项为b1=0，
由bn﹣bn﹣1=n﹣1﹣（n﹣2）=1（n≥2），
可知数列{bn}是以1为公差的等差数列．
∴
【解析】（Ⅰ）设出等比数列的首项和公比，由已知列式求解首项和公比，则其通项公式可求；（Ⅱ）把（Ⅰ）中求得的an代入bn=log3an ，得到数列{bn}的通项公式，由此得到数列{bn}是以0为首项，以1为公差的等差数列，由等差数列的前n项和公式得答案．
【考点精析】解答此题的关键在于理解等差数列的前n项和公式的相关知识，掌握前n项和公式：，以及对等比数列的通项公式（及其变式）的理解，了解通项公式：．

练习册系列答案

相关题目

【题目】如图，多面体中，四边形是菱形，，相交于，，点在平面上的射影恰好是线段的中点.

（Ⅰ）求证：平面；

（Ⅱ）若直线与平面所成的角为，求平面与平面所成角（锐角）的余弦值.

【题目】如图,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C.

(1)当θ=时,求点A的位置,使矩形ABOC的面积最大,并求出这个最大面积;

(2)当θ=时,求点A的位置,使平行四边形ABOC的面积最大,并求出这个最大面积.

【题目】已知向量 =（sin ，sin ）， =（cos ，cos ），且向量与向量共线．
（1）求证：sin（ ﹣ ）=0；
（2）若记函数f（x）=sin（ ﹣ ），求函数f（x）的对称轴方程；
（3）求f（1）+f（2）+f（3）+…+f（2013）的值；
（4）如果已知角0＜A＜B＜π，且A+B+C=π，满足f（）=f（）= ，求的值．