题目内容
16.已知各项均不相等的等差数列{an}的前五项的和为S5=25,且a1,a4,a10成等比数列.(1)求数列{an}的通项公式;
(2)记Tn为数列{$\frac{1}{{a}_{n}•{a}_{n+1}}$}的前n项和,若Tn≤λan+1对?n∈N*都成立,求实数λ的最小值.
分析 (1)设等差数列{an}的公差为d≠0,由a1,a4,a10成等比数列.可得${a}_{4}^{2}$=a1a10,a1=3d.又S5=25,化为a1+2d=5.联立解出即可.
(2)$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{n+2}-\frac{1}{n+3}$,利用“裂项求和”可得数列{$\frac{1}{{a}_{n}•{a}_{n+1}}$}的前n项和Tn=$\frac{1}{3}-\frac{1}{n+3}$.再利用二次函数的单调性即可得出.
解答 解:(1)设等差数列{an}的公差为d≠0,∵a1,a4,a10成等比数列.
∴${a}_{4}^{2}$=a1a10,
∴$({a}_{1}+3d)^{2}$=a1(a1+9d),化为:a1=3d.
又S5=25,∴$5{a}_{1}+\frac{5×4}{2}d$=25,化为a1+2d=5.
联立$\left\{\begin{array}{l}{{a}_{1}=3d}\\{{a}_{1}+2d=5}\end{array}\right.$,解得d=1,a1=3.
∴an=3+(n-1)=n+2.
(2)$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{(n+2)(n+3)}$=$\frac{1}{n+2}-\frac{1}{n+3}$,
∴数列{$\frac{1}{{a}_{n}•{a}_{n+1}}$}的前n项和Tn=$(\frac{1}{3}-\frac{1}{4})$+$(\frac{1}{4}-\frac{1}{5})$+…+$(\frac{1}{n+2}-\frac{1}{n+3})$=$\frac{1}{3}-\frac{1}{n+3}$.
Tn≤λan+1化为:λ≥$-(\frac{1}{n+3})^{2}$+$\frac{1}{3}•\frac{1}{n+3}$=-$(\frac{1}{n+3}-\frac{1}{6})^{2}$+$\frac{1}{36}$.
∴当n=3时,-$(\frac{1}{n+3}-\frac{1}{6})^{2}$+$\frac{1}{36}$取得最大值:$\frac{1}{36}$.
∵Tn≤λan+1对?n∈N*都成立,
∴$λ≥\frac{1}{36}$.
∴实数λ的最小值为$\frac{1}{36}$.
点评 本题考查了等差数列与等比数列的通项公式、“裂项求和”、不等式的性质、二次函数的单调性,考查了推理能力与计算能力,属于难题.

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{2}}{2}$ |
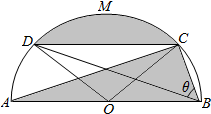 如图:阴影部分是一个机械构件.该构件是由一块半圆形铁皮剪切后,剩下了弓形面CMD,及三角形ABC所形成的.其中半圆直径AB=8,CD∥AB,点M是$\widehat{CD}$上一点,∠CBD=θ.
如图:阴影部分是一个机械构件.该构件是由一块半圆形铁皮剪切后,剩下了弓形面CMD,及三角形ABC所形成的.其中半圆直径AB=8,CD∥AB,点M是$\widehat{CD}$上一点,∠CBD=θ.