题目内容
给出下列命题:(1)函数y=x+
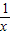 的最小值是2;
的最小值是2; (2)函数y=x+2
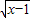 -3的最小值是-2;
-3的最小值是-2;(3)函数
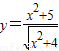 的最小值是
的最小值是 ;
;(4)函数y=
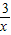 在(-∞,0)∪(0,+∞)内递减;
在(-∞,0)∪(0,+∞)内递减;(5)幂函数y=x3为奇函数且在(-∞,0)内单调递增;
其中真命题的序号有: (把你认为正确的命题的序号都填上)
【答案】分析:对于(1),列举反例x<0时,不成立;对于(2),y=x-1+2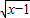 +1-3=
+1-3=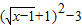 ,配方可求;
,配方可求;
对于(3),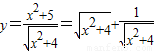 利用基本不等式,等号不可取,当且仅当x=0时函数
利用基本不等式,等号不可取,当且仅当x=0时函数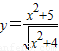 的最小值是
的最小值是 ;对于(4),单调减区间,不可以取并集;对于(5)根据幂函数y=x3的图象可判断.
;对于(4),单调减区间,不可以取并集;对于(5)根据幂函数y=x3的图象可判断.
解答:解:对于(1),x<0时,不成立;
对于(2),y=x-1+2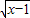 +1-3=
+1-3=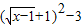 ,∴函数y=x+2
,∴函数y=x+2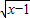 -3的最小值是-2;
-3的最小值是-2;
对于(3),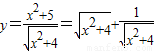 利用基本不等式,等号不可取,当且仅当x=0时函数
利用基本不等式,等号不可取,当且仅当x=0时函数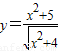 的最小值是
的最小值是 ;
;
对于(4),单调减区间,不可以取并集;
对于(5)根据幂函数y=x3的图象可知正确
故答案为(2)(3)(5)
点评:本题以基本不等式为依托,综合考查函数的性质,有一定的综合性
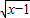 +1-3=
+1-3=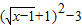 ,配方可求;
,配方可求;对于(3),
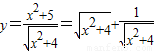 利用基本不等式,等号不可取,当且仅当x=0时函数
利用基本不等式,等号不可取,当且仅当x=0时函数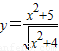 的最小值是
的最小值是 ;对于(4),单调减区间,不可以取并集;对于(5)根据幂函数y=x3的图象可判断.
;对于(4),单调减区间,不可以取并集;对于(5)根据幂函数y=x3的图象可判断.解答:解:对于(1),x<0时,不成立;
对于(2),y=x-1+2
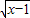 +1-3=
+1-3=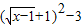 ,∴函数y=x+2
,∴函数y=x+2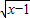 -3的最小值是-2;
-3的最小值是-2;对于(3),
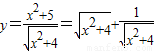 利用基本不等式,等号不可取,当且仅当x=0时函数
利用基本不等式,等号不可取,当且仅当x=0时函数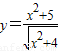 的最小值是
的最小值是 ;
;对于(4),单调减区间,不可以取并集;
对于(5)根据幂函数y=x3的图象可知正确
故答案为(2)(3)(5)
点评:本题以基本不等式为依托,综合考查函数的性质,有一定的综合性

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目