题目内容
(本小题满分12分)
已知数列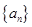 满足
满足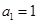 ,
,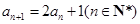 .
.
⑴求证:数列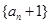 是等比数列,并写出数列
是等比数列,并写出数列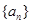 的通项公式;
的通项公式;
⑵若数列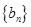 满足
满足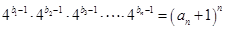 ,求数列
,求数列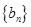 的前n项和
的前n项和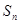 .
.
已知数列
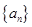 满足
满足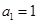 ,
,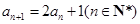 .
.⑴求证:数列
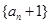 是等比数列,并写出数列
是等比数列,并写出数列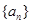 的通项公式;
的通项公式;⑵若数列
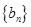 满足
满足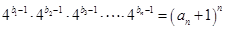 ,求数列
,求数列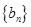 的前n项和
的前n项和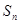 .
.证明:(1)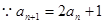 ,
,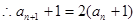 ,
,
又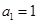 ,∴
,∴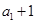 ≠0,
≠0,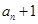 ≠0,∴
≠0,∴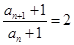 ,
,
∴数列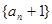 是首项为2,公比为2的等比数列.
是首项为2,公比为2的等比数列.
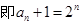 ,因此
,因此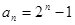 . (6分)
. (6分)
(2)∵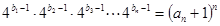 ,∴
,∴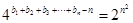 ,
,
∴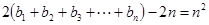 , (10分)
, (10分)
即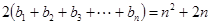 ,∴
,∴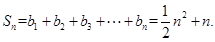 (12分)
(12分)
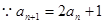 ,
,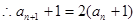 ,
,又
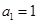 ,∴
,∴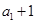 ≠0,
≠0,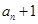 ≠0,∴
≠0,∴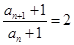 ,
,∴数列
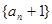 是首项为2,公比为2的等比数列.
是首项为2,公比为2的等比数列.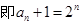 ,因此
,因此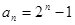 . (6分)
. (6分)(2)∵
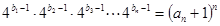 ,∴
,∴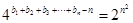 ,
,∴
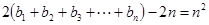 , (10分)
, (10分)即
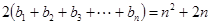 ,∴
,∴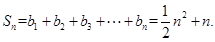 (12分)
(12分)略

练习册系列答案
相关题目
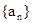 的公差
的公差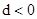 , 若
, 若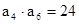 ,
, 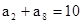 , 则该数列的前n项和
, 则该数列的前n项和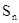 的最大值为 ( )
的最大值为 ( ) 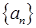 的前
的前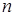 项和
项和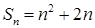 ,设数列
,设数列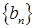 满足
满足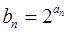 ,
,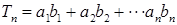 ,求
,求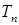
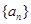 的前
的前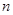 项和为
项和为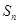 ,且
,且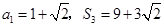 .
.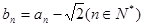 ,
,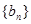 中的部分项
中的部分项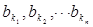 恰好组成等比数列,且
恰好组成等比数列,且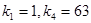 ,求该等比数列的公比与数列
,求该等比数列的公比与数列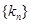 的通项公式。
的通项公式。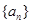 中,
中,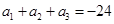 ,
,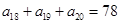 ,则此数列前
,则此数列前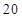 项和等于( )
项和等于( )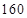
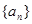 的前13项之和为
的前13项之和为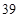 ,则
,则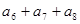 等于( )
等于( )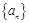 的前
的前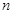 项和为
项和为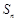 ,
,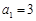 ,且当
,且当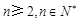 时
时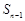 是
是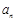 与
与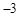 的等差中项,则数列
的等差中项,则数列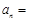 .
.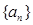 中,
中,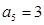 ,
,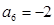 ,则
,则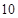 项和
项和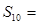 __________
__________