题目内容
(本小题满分12分)
如图椭圆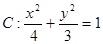 的右顶点是
的右顶点是 ,上下两个顶点分别为
,上下两个顶点分别为 ,四边形
,四边形 是矩形(
是矩形(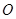 为原点),点
为原点),点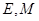 分别为线段
分别为线段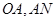 的中点.
的中点.

(Ⅰ)证明:直线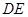 与直线
与直线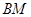 的交点在椭圆
的交点在椭圆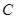 上;
上;
(Ⅱ)若过点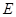 的直线交椭圆于
的直线交椭圆于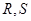 两点,
两点,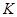 为
为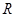 关于
关于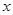 轴的对称点(
轴的对称点(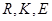 不共线),
不共线),
问:直线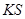 是否经过
是否经过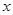 轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.
轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.
【答案】
(Ⅰ)见解析;
(Ⅱ)直线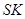 经过
经过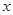 轴上的点
轴上的点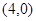
【解析】(1)易求A、B、D、E、M的坐标,然后求出DE、BM的方程,两直线方程联立解方程组可求出其交点.再验证交点坐标满足椭圆方程,从而证明交点在椭圆上.
(2)先设出RS的方程,与椭圆方程联立,消y后得关于x的一元二次方程,设出交点R、S的坐标,表示出SK的方程,令y=0得到它与x轴的交点的模坐标 ,然后再借助直线RS的方程和韦达定理,证明x的值是常数即可.
,然后再借助直线RS的方程和韦达定理,证明x的值是常数即可.
解:(1)由题意,得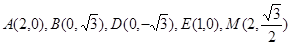 ,
,
所以直线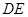 的方程
的方程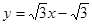 ,直线
,直线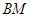 的方程为
的方程为 ,------2分
,------2分
由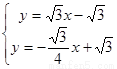 ,得
,得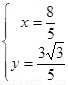 ,
,
所以直线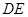 与直线
与直线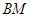 的交点坐标为
的交点坐标为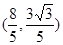 ,---------------4分
,---------------4分
因为 ,所以点
,所以点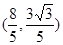 在椭圆
在椭圆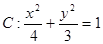 上.---------6分
上.---------6分
(2)设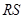 的方程为
的方程为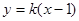 ,代入
,代入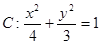 ,
,
得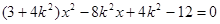 ,
,
设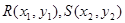 ,则
,则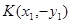 ,
,
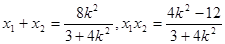 ,
,
直线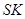 的方程为
的方程为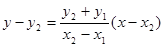 ,
,
令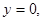 得
得 ,
,
将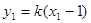 ,
, 代入上式得,设
代入上式得,设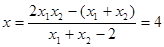 ,
,
所以直线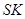 经过
经过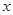 轴上的点
轴上的点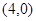 .---------12分
.---------12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目