题目内容
(本题满分18分)第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分。
圆锥曲线上任意两点连成的线段称为弦。若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦。已知椭圆C:![]() 。
。
 (1)过椭圆C的右焦点作一条垂直于
(1)过椭圆C的右焦点作一条垂直于![]() 轴的垂轴弦
轴的垂轴弦![]() ,求
,求![]() 的长度;
的长度;
(2)若点![]() 是椭圆C上不与顶点重合的任意一点,
是椭圆C上不与顶点重合的任意一点,![]() 是椭圆C的短轴,直线
是椭圆C的短轴,直线![]() 分别交
分别交![]() 轴于点
轴于点![]() 和点
和点![]() (如右图),求
(如右图),求![]() 的值;
的值;
(3)在(2)的基础上,把上述椭圆C一般化为![]() ,
,![]() 是任意一条垂直于
是任意一条垂直于![]() 轴的垂轴弦,其它条件不变,试探究
轴的垂轴弦,其它条件不变,试探究![]() 是否为定值?(不需要证明);请你给出双曲线
是否为定值?(不需要证明);请你给出双曲线![]() 中相类似的结论,并证明你的结论。
中相类似的结论,并证明你的结论。
(1)由条件可知右焦点的坐标为![]() ……………. 1分
……………. 1分
![]() 代入椭圆C的方程
代入椭圆C的方程![]() ,得
,得![]() ……………. 3分
……………. 3分
所以![]() ……………. 4分
……………. 4分
(2)设![]()
则![]() ……………. 6分
……………. 6分
令![]() 则
则![]() ……………. 7分
……………. 7分
同理可得:![]() ,
,![]() …………….8分
…………….8分
![]() 在椭圆C:
在椭圆C:![]() 上,
上,![]() ,
,
则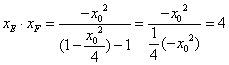 ……………. 10分
……………. 10分
(3)点![]() 是椭圆C:
是椭圆C:![]() 上不与顶点重合的任意一点,
上不与顶点重合的任意一点,![]() 是垂直于
是垂直于![]() 轴的垂轴弦,直线
轴的垂轴弦,直线![]() 分别交
分别交![]() 轴于点
轴于点![]() 和点
和点![]() ,则
,则![]() 。……… 12分
。……… 12分
点![]() 是双曲线C:
是双曲线C:![]() 上不与顶点重合的任意一点,
上不与顶点重合的任意一点,![]() 是垂直于
是垂直于![]() 轴的垂轴弦,直线
轴的垂轴弦,直线![]() 分别交
分别交![]() 轴于点
轴于点![]() 和点
和点![]() ,则
,则![]() 。……………. 14分
。……………. 14分
证明如下:设![]()
则 ![]()
令![]() 则
则![]()
同理可得:![]() ,
,![]()
![]() 在双曲线C:
在双曲线C:![]() 上,
上,![]() ,
,
则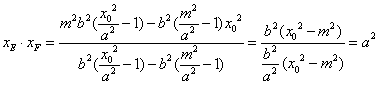 ……………. 18分
……………. 18分

练习册系列答案
相关题目
 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当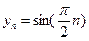 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
( 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
. ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
( ,
,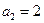 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
(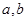 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
.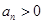 ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
(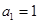 ,
,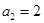 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,其中
,其中 .
. 时,设
时,设 ,
, ,求
,求 的解析式及定义域;
的解析式及定义域; 时,求
时,求 的最小值;
的最小值; ,当
,当 时,
时, 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围. 是等差数列,且公差为
是等差数列,且公差为 ,若数列
,若数列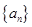 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”. ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”; 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么? 是数列
是数列 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使 ;若存在,求
;若存在,求