题目内容
4.设函数f(x)=ex+$\frac{x}{x+1}$.(1)求证:函数f(x)的唯一零点x0∈(-$\frac{1}{2}$,0);
(2)求证:对任意λ>0,存在μ<0,使得f(x)<0在(-1,λμ)上恒成立;
(3)设g(x)=f(x)-x=($\frac{1}{2}$)h(x)-1,当x>0时,比较g(x)与h(x)的大小.
分析 (1)令f(x)=0,可得ex=-$\frac{x}{x+1}$,由ex>0,可得-1<x<0,运用零点存在定理,即可得证;
(2)运用(1)的结论,结合f(x)<0,在(-1,x0)处恒成立.即可得证;
(3)求出g(x)的导数,判断单调性,可得g(x)>0,运用复合函数的单调性可得h(x)的单调性,可得h(x)<0,即可得到结论.
解答 解:(1)证明:令f(x)=0,可得ex=-$\frac{x}{x+1}$,
由ex>0,可得-1<x<0,
由f(x)=ex+$\frac{x}{x+1}$=ex+1-$\frac{1}{1+x}$在(-$\frac{1}{2}$,0)递增,
由f(-$\frac{1}{2}$)=${e}^{-\frac{1}{2}}$+1-$\frac{1}{1-\frac{1}{2}}$=${e}^{-\frac{1}{2}}$-1<0,
f(0)=1+0>0,由函数零点存在定理,可得
函数f(x)存在唯一零点x0∈(-$\frac{1}{2}$,0);
(2)证明:由(1)可得f(x)在(-1,0)递增,
由函数f(x)存在唯一零点x0∈(-$\frac{1}{2}$,0),
即有f(x)<0,在(-1,x0)处恒成立.
可令λμ=x0,即有对任意λ>0,存在μ<0,
使得f(x)<0在(-1,λμ)上恒成立;
(3)g(x)=f(x)-x=ex+$\frac{x}{x+1}$-x=ex+1-$\frac{1}{x+1}$-x
的导数为g′(x)=ex+$\frac{1}{(x+1)^{2}}$-1,
x>0时,ex>1,g′(x)>0,g(x)递增,即有g(x)>g(0)=1,
h(x)=$lo{g}_{\frac{1}{2}}$g(x)+1在x>0时,由t=g(x)在x>0递增,
h(x)=1+$lo{g}_{\frac{1}{2}}$t递减,即有h(x)在x>0递减,
则h(x)<h(0)=1,
故当x>0时,g(x)>h(x).
点评 本题考查导数的运用:求单调区间,考查函数零点存在定理的运用,以及函数的单调性的运用,属于中档题.

| A. | ?x0∈N,x02+2x0≤3 | B. | ?x∈N,x2+2x≤3 | C. | ?x0∈N,x02+2x0<3 | D. | ?x∈N,x2+2x<3 |
| A. | 0<x0<$\frac{1}{4}$ | B. | $\frac{1}{4}$<x0<$\frac{1}{3}$ | C. | $\frac{1}{3}$<x0<$\frac{1}{2}$ | D. | $\frac{1}{2}$<x0<1 |
| A. | f(x)=4x2-6 | B. | f(x)=$\frac{1}{4}{x}^{2}-\frac{3}{2}x-\frac{15}{4}$ | ||
| C. | f(x)=$\frac{1}{4}{x}^{2}+\frac{3}{2}x-\frac{15}{4}$ | D. | f(x)=x2-2x-5 |
| A. | ∅∈A | B. | 0∈A | C. | -1∈A | D. | {-1}⊆A |
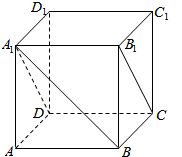 在正方体ABCD-A1B1C1D1中.
在正方体ABCD-A1B1C1D1中.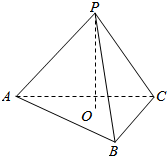 如图,三棱锥P-ABC的三条侧棱两两垂直,即:PA⊥PB、PB⊥PC、PC⊥PA,且PO⊥平面ABC并交平面ABC于点O,请问点O是△ABC的什么心(内心、外心、垂心、重心、中心等)?并证明你的结论.
如图,三棱锥P-ABC的三条侧棱两两垂直,即:PA⊥PB、PB⊥PC、PC⊥PA,且PO⊥平面ABC并交平面ABC于点O,请问点O是△ABC的什么心(内心、外心、垂心、重心、中心等)?并证明你的结论.