Question

13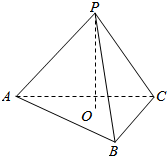．如图，三棱锥P-ABC的三条侧棱两两垂直，即：PA⊥PB、PB⊥PC、PC⊥PA，且PO⊥平面ABC并交平面ABC于点O，请问点O是△ABC的什么心（内心、外心、垂心、重心、中心等）？并证明你的结论．

Answer 1

分析 本题是立体几何中一道证明题，点P为△ABC所在平面外一点，PO⊥平面ABC，垂足为O，从而证得BC⊥AE、AB⊥CF，符合这一性质的点O是△ABC垂心．

解答 解：垂心，（2分）
证明如下：
连接AO交BC于点E，连接PE，连接CO交AB于点F，
PA⊥PB、PC⊥PA，PB∩PC=P，故PA⊥平面PBC，
BC?平面PBC，故PA⊥BC，①（6分）
由PO⊥平面ABC，BC?平面ABC，故PO⊥BC，②
由①②及PA∩PO=P，故有BC⊥平面PAE，（11分）
AE?平面PAE，故BC⊥AE，（12分）
同理：AB⊥CF，
因而点O是△ABC的垂心．（14分）
〖注〗来自课本

点评 本题主要考查了直线与平面垂直的性质，考查了空间想象能力和推理论证能力，属于中档题．