题目内容
(2010•沅江市模拟)椭圆b2x2+a2y2=a2b2(a>b>0)的两个焦点分别是F1、F2,等边三角形的边AF1、AF2与该椭圆分别相交于B、C两点,且2|BC|=|F1F2|,则该椭圆的离心率等于( )
分析:由△A为正三角形可得∠AF1F2=∠A=60°,则可求直线AF1,AF2的斜率,进而可求所在的直线方程,其交点,而AF1中点B在椭圆上,代入椭圆的方程,结合b2=a2-c2及0<e<1可求该椭圆的离心率.
解答: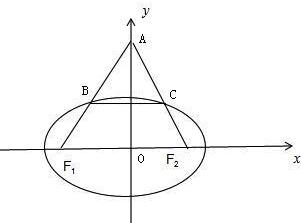 解:由△AF1F2为正三角形可得∠AF1F2=∠AF2F1=60°
解:由△AF1F2为正三角形可得∠AF1F2=∠AF2F1=60°
则直线AF1,AF2的斜率分别为
,-
则直线AF1,AF2所在的直线方程分别为y=
(x+c),y=-
(x-c),
其交点A(0,
c),由于2|BC|=|F1F2|,得BC是三角形的中位线,得B是AF1的中点,
从而AF1中点B( -
c,
c)在椭圆上,代入椭圆的方程可得
+
=1
整理可得,c2(a2-c2)+3c2a2=4a2(a2-c2)
∴4a4-8a2c2+c4=0
两边同时除以a4可得,e4-8e2+4=0
∵0<e<1
∴e2=4-2
,e2=2+
(舍)
∴e=
-1
故选C.
 解:由△AF1F2为正三角形可得∠AF1F2=∠AF2F1=60°
解:由△AF1F2为正三角形可得∠AF1F2=∠AF2F1=60°则直线AF1,AF2的斜率分别为
| 3 |
| 3 |
则直线AF1,AF2所在的直线方程分别为y=
| 3 |
| 3 |
其交点A(0,
| 3 |
从而AF1中点B( -
| 1 |
| 2 |
| ||
| 2 |
| c2 |
| 4a2 |
| 3c2 |
| 4b2 |
整理可得,c2(a2-c2)+3c2a2=4a2(a2-c2)
∴4a4-8a2c2+c4=0
两边同时除以a4可得,e4-8e2+4=0
∵0<e<1
∴e2=4-2
| 3 |
| 3 |
∴e=
| 3 |
故选C.
点评:本题考查椭圆的简单性质,直角三角形中的边角关系的应用,考查计算能力和数形结合思想.

练习册系列答案
相关题目