题目内容
15．函数f（x）=2x+lg（x+1）-5的零点x0∈（k，k+1），k∈Z，则k=2．分析 可判断函数f（x）=2x+lg（x+1）-5在其定义域上连续单调递增，从而解得．
解答 解：函数f（x）=2x+lg（x+1）-5在其定义域上连续单调递增，
f（2）=4+lg3-5＜0，f（3）=8+lg4-5＞0，
故f（2）f（3）＜0，
故x0∈（2，3），
故答案为：2．
点评 本题考查了函数的单调性的判断与函数零点的判定定理的应用．
练习册系列答案
发散思维新课堂系列答案
相关题目
如图，正方体棱长为4，M，P分别为A1B1，B1C1的中点，设点D，M，P三点的平面与棱CC1交于点N，求PM+PN的值．
3．若偶函数f（x）在（-∞，0]上单调递减，a=f（log23），b=f（log45），c=f（2${\;}^{\frac{3}{2}}$），则a，b，c满足（ ）
| A． | a＜b＜c | B． | b＜a＜c | C． | c＜a＜b | D． | c＜b＜a |
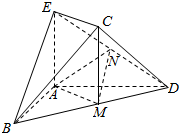如图，在几何体ABDCE中，AB=AD，AE⊥平面ABD，M为线段BD的中点，MC∥AE，AE=MC．