题目内容
已知△ABC外接圆半径为1,且acosB+bcosA=2,则△ABC是( )
分析:由正弦定理以及 acosB+bcosA=2,可得 2RsinAcosB+2RsinBcosA=2R,sin(A+B)=1,故有sinC=1,C=
,故△ABC为直角三角.
| π |
| 2 |
解答:解:由于△ABC外接圆半径为R=1,由正弦定理可得 a=2RsinA2sinA,b=2RsinB=2sinB,
再由 acosB+bcosA=2,可得 2RsinAcosB+2RsinBcosA=2R,∴sin(A+B)=1,故有sinC=1,
∴C=
,故△ABC为直角三角,
故选B.
再由 acosB+bcosA=2,可得 2RsinAcosB+2RsinBcosA=2R,∴sin(A+B)=1,故有sinC=1,
∴C=
| π |
| 2 |
故选B.
点评:本题主要考查正弦定理、诱导公式的应用,属于中档题.

练习册系列答案
相关题目
在△ABC中,已知a=2,30°≤A≤150°,则△ABC外接圆半径取值范围是( )
| A、[1,2] | ||||
B、[1,
| ||||
C、[
| ||||
| D、[1,+∞) |
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.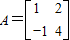
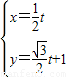 (t为参数),求直线l被曲线C截得的线段长度.
(t为参数),求直线l被曲线C截得的线段长度.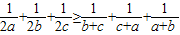 .
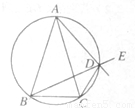
.

 (t为参数),求直线l被曲线C截得的线段长度.
(t为参数),求直线l被曲线C截得的线段长度. .
.