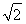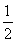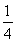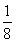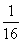题目内容
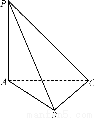
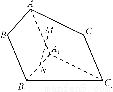
如图所示,在三棱柱ABCA1B1C1中,M、N分别是BC和A1B1的中点.求证:MN∥平面AA1C1.
见解析
【解析】证明:设A1C1中点为F,连结NF、FC.
∵N为A1B1中点,∴NF∥B1C1,且NF=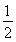 B1C1.又由棱柱性质知B1C1∥=BC,又M是BC的中点,∴NF∥=MC,∴四边形NFCM为平行四边形.
B1C1.又由棱柱性质知B1C1∥=BC,又M是BC的中点,∴NF∥=MC,∴四边形NFCM为平行四边形.
∴MN∥CF.又CF?平面AA1C1,MN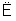 平面AA1C1,∴MN∥平面AA1C1
平面AA1C1,∴MN∥平面AA1C1

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目