题目内容
已知直线l:y=kx+1,椭圆E: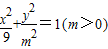 .
.(Ⅰ)若不论k取何值,直线l与椭圆E恒有公共点,试求出m的取值范围及椭圆离心率e关于m的函数关系式;
(Ⅱ)当
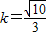 时,直线l与椭圆E相交于A,B两点,与y轴交于点M.若
时,直线l与椭圆E相交于A,B两点,与y轴交于点M.若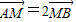 ,求椭圆E的方程.
,求椭圆E的方程.
【答案】分析:(Ⅰ)由直线l恒过定点M(0,1),且直线l与椭圆E恒有公共点,知点M(0,1)在椭圆E上或其内部,得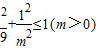 ,由此能求出求出m的取值范围及椭圆离心率e关于m的函数关系式.
,由此能求出求出m的取值范围及椭圆离心率e关于m的函数关系式.
(Ⅱ)由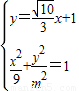 ,消去y得
,消去y得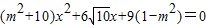 .设A(x1,y1),B(x2,y2),则
.设A(x1,y1),B(x2,y2),则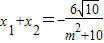 ,
,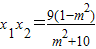 .M(0,1),由
.M(0,1),由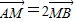 得x1=-2x2.由此得
得x1=-2x2.由此得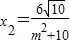 .从而得到椭圆E的方程.
.从而得到椭圆E的方程.
解答:解:(Ⅰ)∵直线l恒过定点M(0,1),且直线l与椭圆E恒有公共点,
∴点M(0,1)在椭圆E上或其内部,得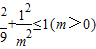 ,
,
解得m≥1,且m≠3.(3分)
(联立方程组,用判别式法也可)
当1≤m<3时,椭圆的焦点在x轴上,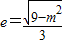 ;
;
当m>3时,椭圆的焦点在y轴上,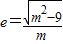 .
.
∴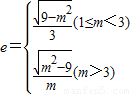 (6分)
(6分)
(Ⅱ)由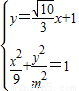 ,消去y得
,消去y得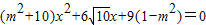 .
.
设A(x1,y1),B(x2,y2),则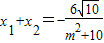 ①,
①,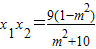 ②.
②.
∵M(0,1),∴由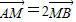 得x1=-2x2③.(9分)
得x1=-2x2③.(9分)
由①③得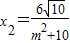 ④.
④.
将③④代入②得,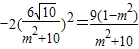 ,解得m2=6(m2=-15不合题意,舍去).
,解得m2=6(m2=-15不合题意,舍去).
∴椭圆E的方程为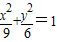 .(12分)
.(12分)
点评:本题考查椭圆方程的求法和求出m的取值范围及椭圆离心率e关于m的函数关系式.解题时要认真审题,合理地进行等价转化,提高解题能力和解题技巧.
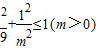 ,由此能求出求出m的取值范围及椭圆离心率e关于m的函数关系式.
,由此能求出求出m的取值范围及椭圆离心率e关于m的函数关系式.(Ⅱ)由
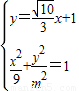 ,消去y得
,消去y得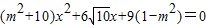 .设A(x1,y1),B(x2,y2),则
.设A(x1,y1),B(x2,y2),则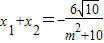 ,
,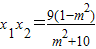 .M(0,1),由
.M(0,1),由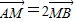 得x1=-2x2.由此得
得x1=-2x2.由此得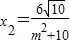 .从而得到椭圆E的方程.
.从而得到椭圆E的方程.解答:解:(Ⅰ)∵直线l恒过定点M(0,1),且直线l与椭圆E恒有公共点,
∴点M(0,1)在椭圆E上或其内部,得
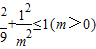 ,
,解得m≥1,且m≠3.(3分)
(联立方程组,用判别式法也可)
当1≤m<3时,椭圆的焦点在x轴上,
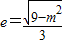 ;
;当m>3时,椭圆的焦点在y轴上,
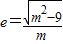 .
.∴
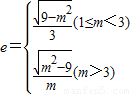 (6分)
(6分)(Ⅱ)由
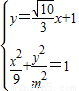 ,消去y得
,消去y得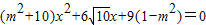 .
.设A(x1,y1),B(x2,y2),则
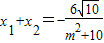 ①,
①,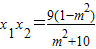 ②.
②.∵M(0,1),∴由
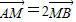 得x1=-2x2③.(9分)
得x1=-2x2③.(9分)由①③得
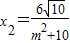 ④.
④.将③④代入②得,
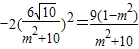 ,解得m2=6(m2=-15不合题意,舍去).
,解得m2=6(m2=-15不合题意,舍去).∴椭圆E的方程为
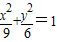 .(12分)
.(12分)点评:本题考查椭圆方程的求法和求出m的取值范围及椭圆离心率e关于m的函数关系式.解题时要认真审题,合理地进行等价转化,提高解题能力和解题技巧.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足
如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足