题目内容
已知函数f(x)=asinx-x+b(a、b均为正常数).
(1)证明函数f(x)在(0,a+b]内至少有一个零点;
(2)设函数f(x)在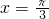 处有极值,对于一切
处有极值,对于一切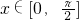 ,不等式f(x)>sinx+cosx总成立,求b的取值范围.
,不等式f(x)>sinx+cosx总成立,求b的取值范围.
解:(1)∵f(0)=b>0…
f(a+b)=asin(a+b)-(a+b)+b=a[sin(a+b)-1]≤0…
∴函数f(x)在(0,a+b]内至少有一个零点…
(2)∵f(x)=asinx-x+b,∴f'(x)=acosx-1…
由题意得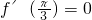 ,即
,即 …
…
问题等价于b>x+cosx-sinx对一切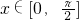 恒成立…
恒成立…
记g(x)=x+cosx-sinx,
则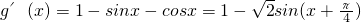 …
…
∵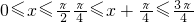 …
…
∴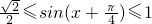
即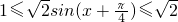
∴g'(x)≤0,即g(x)在 上是减函数…
上是减函数…
∴g(x)max=g(0)=1,于是b>1,故b的取值范围是(1,+∞)…
分析:(1)函数f(x)=asinx-x+b在(0,a+b]内至少有一个零点,代入f(0)和f(a+b)利用零点定理进行求解;
(2)对f(x)进行求导,利用函数f(x)在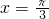 处有极值,可得f′(
处有极值,可得f′( )=0,求出a的值,将问题转化为b>x+cosx-sinx对一切
)=0,求出a的值,将问题转化为b>x+cosx-sinx对一切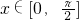 恒成立,利用常数分离法进行求解;
恒成立,利用常数分离法进行求解;
点评:此题主要考查函数的零点定理以及函数的恒成立问题,利用导数研究函数的最值和极值问题,是一道基础题;
f(a+b)=asin(a+b)-(a+b)+b=a[sin(a+b)-1]≤0…
∴函数f(x)在(0,a+b]内至少有一个零点…
(2)∵f(x)=asinx-x+b,∴f'(x)=acosx-1…
由题意得
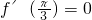 ,即
,即 …
…问题等价于b>x+cosx-sinx对一切
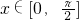 恒成立…
恒成立…记g(x)=x+cosx-sinx,
则
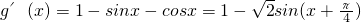 …
…∵
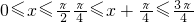 …
…∴
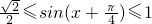
即
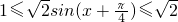
∴g'(x)≤0,即g(x)在
 上是减函数…
上是减函数…∴g(x)max=g(0)=1,于是b>1,故b的取值范围是(1,+∞)…
分析:(1)函数f(x)=asinx-x+b在(0,a+b]内至少有一个零点,代入f(0)和f(a+b)利用零点定理进行求解;
(2)对f(x)进行求导,利用函数f(x)在
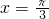 处有极值,可得f′(
处有极值,可得f′( )=0,求出a的值,将问题转化为b>x+cosx-sinx对一切
)=0,求出a的值,将问题转化为b>x+cosx-sinx对一切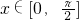 恒成立,利用常数分离法进行求解;
恒成立,利用常数分离法进行求解;点评:此题主要考查函数的零点定理以及函数的恒成立问题,利用导数研究函数的最值和极值问题,是一道基础题;

练习册系列答案
相关题目