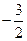题目内容
已知直线 过定点
过定点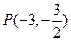 与圆
与圆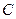 :
: 相交于
相交于 、
、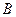 两点.
两点.
求:(1)若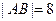 ,求直线
,求直线 的方程;
的方程;
(2)若点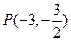 为弦
为弦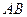 的中点,求弦
的中点,求弦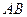 的方程.
的方程.
 过定点
过定点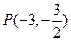 与圆
与圆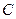 :
: 相交于
相交于 、
、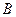 两点.
两点.求:(1)若
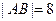 ,求直线
,求直线 的方程;
的方程;(2)若点
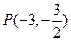 为弦
为弦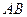 的中点,求弦
的中点,求弦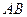 的方程.
的方程.(1)直线 的方程为
的方程为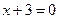 或
或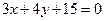 .(2)弦
.(2)弦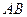 的方程为
的方程为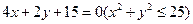 .
.
 的方程为
的方程为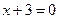 或
或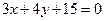 .(2)弦
.(2)弦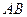 的方程为
的方程为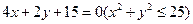 .
. (1)由圆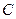 的参数方程
的参数方程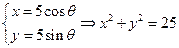 ,
,
设直线 的参数方程为①
的参数方程为①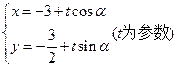 ,
,
将参数方程①代入圆的方程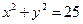
得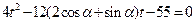 ,
,
∴△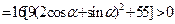 ,
,
所以方程有两相异实数根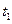 、
、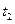 ,
,
∴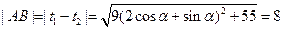 ,
,
化简有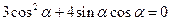 ,
,
解之 或
或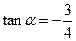 ,
,
从而求出直线 的方程为
的方程为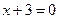 或
或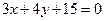 .
.
(2)若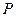 为
为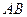 的中点,所以
的中点,所以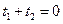 ,
,
由(1)知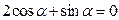 ,得
,得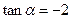 ,
,
故所求弦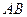 的方程为
的方程为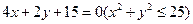 .
.
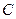 的参数方程
的参数方程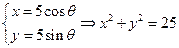 ,
, 设直线
 的参数方程为①
的参数方程为①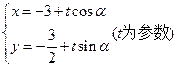 ,
,将参数方程①代入圆的方程
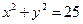
得
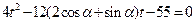 ,
,∴△
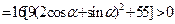 ,
,所以方程有两相异实数根
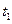 、
、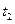 ,
,∴
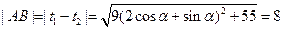 ,
,化简有
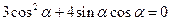 ,
,解之
 或
或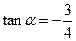 ,
,从而求出直线
 的方程为
的方程为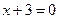 或
或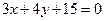 .
.(2)若
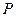 为
为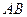 的中点,所以
的中点,所以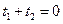 ,
,由(1)知
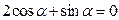 ,得
,得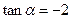 ,
,故所求弦
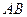 的方程为
的方程为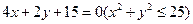 .
.
练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
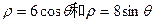 ,求这两个圆的圆心距。
,求这两个圆的圆心距。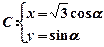 (
(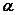 为参数); 直线
为参数); 直线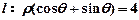 .
.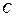 的普通方程和直线l的直角坐标方程;
的普通方程和直线l的直角坐标方程;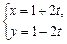 (t为参数)被圆
(t为参数)被圆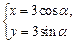 (α为参数)截得的弦长.
(α为参数)截得的弦长.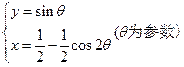 与直线
与直线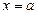 有两个不同的公共点,则实数
有两个不同的公共点,则实数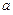 的取值范围是_________________.
的取值范围是_________________.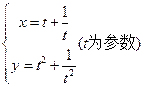 化为普通方程,所得方程是 _________.
化为普通方程,所得方程是 _________. .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 ,则直线
,则直线 ,且
,且 ,则
,则 的最小值为 .
的最小值为 .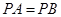 ,
, ,
, 与
与 交于点D,且
交于点D,且 ,
, ,则
,则 .
.
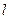 的参数方程是
的参数方程是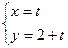 (
(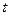 是参数),以原点
是参数),以原点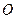 为极点,
为极点,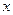 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆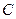 的极坐标方程为
的极坐标方程为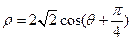 ,则圆
,则圆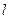 的距离是 .
的距离是 . ,则直线的斜率为( )
,则直线的斜率为( )