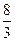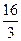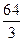题目内容
．在矩形ABCD中，AB = 
4，BC = 3，沿对角线AC把矩形折成二面角D-AC-B，并且
D点在平面ABC内的射影落在AB上．若在四面体D-
ABC内有一球，当球的体积最大时，球的半径是 .
4，BC = 3，沿对角线AC把矩形折成二面角D-AC-B，并且D点在平面ABC内的射影落在AB上．若在四面体D-ABC内有一球，当球的体积最大时，球的半径是 . 当球的体积最大时，球与三棱锥D -ABC 的各面相切，设球队半径为R ，则VD -ABC =" VO" -ABC +VO -DAC + VO -DBA + VO -DAB = R(S△ABC + S△DAC + S△DBC + S△DAB).由题设易知AD⊥平面DBC, 又∵BD
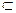平面DBC，∴AD⊥BD，∴△ABD为直角三角形，∵AB = 4，AD = 3，∴BD = ，∴S△ABC = AD·BD = ×3×= .在△DAB和△DBC中，∵AD = BC，AB = DC，DB = DB，∴△DAB
≌△BCD，故S△DBC = ，VD -ABC =" VA" –DBC = ×3×= ，∴S△ABC = S△ADC = 6，∴R(6 + 6 +
+ )，于是( 4 + )R = 
， 解得R =
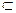C, 又∵BD平面DBC，∴AD⊥BD，∴△ABD为直角三角形，∵AB = 4，AD = 3，∴BD = ，∴S△ABC = AD·BD = ×3×= .在△DAB和△DBC中，∵AD = BC，AB = DC，DB = DB，∴△DAB≌△BCD，故S△DBC = ，VD -ABC =" VA" –DBC = ×3×= ，∴S△ABC = S△ADC = 6，∴R(6 + 6 ++ )，于是( 4 + )R = ， 解得R = 
练习册系列答案
相关题目
中，二面角
的平面角等于 （ ）
B.
C .
D 
中，
是
的中点，沿
将
折起，使二面角
为60°，则四棱锥
的体积是
，
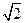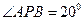，点E、F分别在侧棱PB、PC上，则
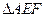周长的最小值为 .
.
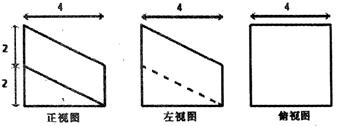
中，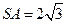
， AB=4，则三棱锥A-SBC的体积为
