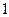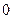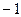题目内容
定义在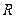 上的函数
上的函数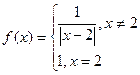 ,若关于
,若关于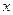 的
的
方程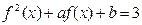 ,有3个不同实数解
,有3个不同实数解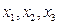 ,且
,且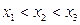 ,则下列说法中正确的是:( )
,则下列说法中正确的是:( )
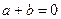
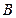
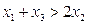
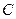
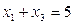
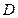
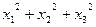
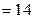
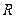 上的函数
上的函数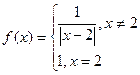 ,若关于
,若关于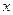 的
的方程
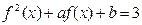 ,有3个不同实数解
,有3个不同实数解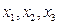 ,且
,且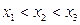 ,则下列说法中正确的是:( )
,则下列说法中正确的是:( )
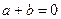
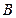
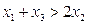
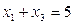
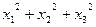
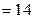
D
有三个根,故必有一根是2,且其他两根必有一根小于2,一根大于2,
由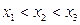 ,可知
,可知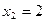
当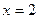 时,
时,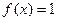 ,代入可得
,代入可得 ,所以
,所以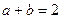
不妨设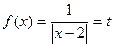
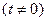
则方程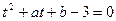 有唯一解(若
有唯一解(若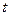 有两解,则对应的
有两解,则对应的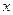 有4个)
有4个)
从而△=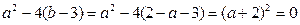
所以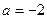 ,从而
,从而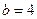 ,此时方程变为
,此时方程变为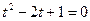 所以
所以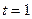 ,
,
即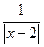 =1,解得
=1,解得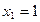 ,
,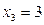 ,又
,又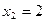 ,所以
,所以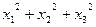
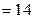 ,选D
,选D
由
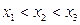 ,可知
,可知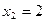
当
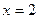 时,
时,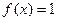 ,代入可得
,代入可得 ,所以
,所以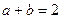
不妨设
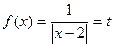
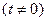
则方程
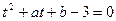 有唯一解(若
有唯一解(若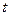 有两解,则对应的
有两解,则对应的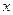 有4个)
有4个)从而△=
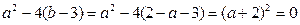
所以
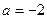 ,从而
,从而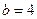 ,此时方程变为
,此时方程变为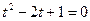 所以
所以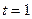 ,
,即
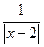 =1,解得
=1,解得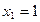 ,
,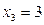 ,又
,又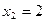 ,所以
,所以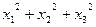
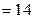 ,选D
,选D
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
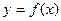 ,
,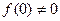 ,当
,当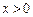 时,
时,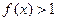 ,且
,且 ∈R,有
∈R,有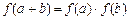 .
. ;
;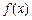 是R上的增函数;
是R上的增函数;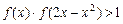 ,求
,求 的取值范围.
的取值范围.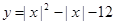 两个零点的差的绝对值是( ).
两个零点的差的绝对值是( ).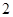

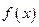 是偶函数,并且对于定义域内任意的
是偶函数,并且对于定义域内任意的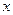 ,满足
,满足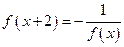 ,
,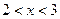 时,
时,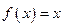 ,则
,则 =__________ ______.
=__________ ______.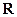 上的函数
上的函数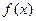 满足
满足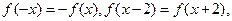 且
且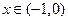 时,
时,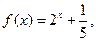 则
则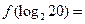
 B
B  C
C 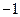 D
D 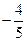
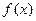 是在
是在 上的偶函数,且在
上的偶函数,且在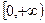 时,函数
时,函数 的解集是:( )
的解集是:( )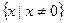
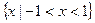
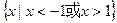
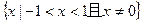
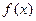 满足
满足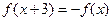 ,当
,当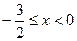 时,
时,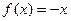 ,
,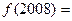 ( )
( )