题目内容
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<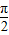 )的图象如图所示.
)的图象如图所示.(1)求f(x)的解析式;
(2)将函数y=f(x)的图象向右平移
 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的对称轴方程;
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的对称轴方程;(3)当
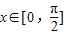 时,方程f(x)=2a-3有两个不等的实根x1,x2,求实数a的取值范围,并求此时x1+x2的值.
时,方程f(x)=2a-3有两个不等的实根x1,x2,求实数a的取值范围,并求此时x1+x2的值.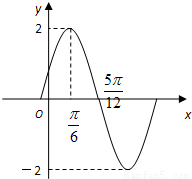
【答案】分析:(1)由图知,A=2,由T=π,可求得ω,由2sin(2×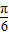 +φ)=2可求得φ;
+φ)=2可求得φ;
(2)由函数y=Asin(ωx+φ)的图象变换可求得g(x)=2sin(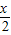 -
-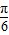 ),由正弦函数的性质即可求得g(x)的对称轴方程;
),由正弦函数的性质即可求得g(x)的对称轴方程;
(3)由x∈[0,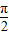 ]⇒2x+
]⇒2x+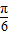 ∈[
∈[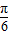 ,
,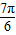 ],方程f(x)=2a-3有两个不等实根时,y=f(x)的图象与直线y=2a-3有两个不同的交点,从而可求得a的取值范围;
],方程f(x)=2a-3有两个不等实根时,y=f(x)的图象与直线y=2a-3有两个不同的交点,从而可求得a的取值范围;
(法一)当x∈[0,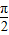 ],时,利用f(x1)=f(x2),即可求得x1+x2的值;
],时,利用f(x1)=f(x2),即可求得x1+x2的值;
(法二)令2x+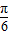 =
=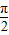 +kπ,可求得x=
+kπ,可求得x=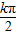 +
+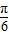 ,(k∈Z),利用f(x)的对称轴方程为x=
,(k∈Z),利用f(x)的对称轴方程为x=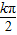 +
+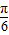 即可求得x1+x2的值.
即可求得x1+x2的值.
解答:解:(1)由图知,A=2.--------(1分)
T=π,ω=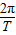 =
=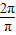 =2-----(2分)
=2-----(2分)
由2sin(2×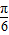 +φ)=2,即sin(
+φ)=2,即sin(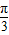 +φ)=1,故
+φ)=1,故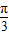 +φ=
+φ=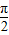 +2kπ,k∈Z,
+2kπ,k∈Z,
所以φ=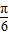 +2kπ,k∈Z,
+2kπ,k∈Z,
又φ∈(0,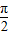 ),所以φ=
),所以φ=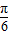 ---(3分)
---(3分)
故f(x)=2sin(2x+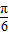 )-------(4分)
)-------(4分)
(2)将f(x)的图象向右平移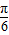 个单位后,得到f(x-
个单位后,得到f(x-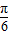 )的图象,再将所得图象横坐标伸长到原来的4倍,
)的图象,再将所得图象横坐标伸长到原来的4倍,
纵坐标不变,得到f(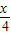 -
-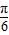 )的图象,
)的图象,
所以g(x)=f(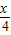 -
-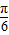 )=2sin[2(
)=2sin[2(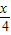 -
-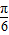 )+
)+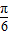 )]=2sin(
)]=2sin(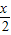 -
-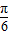 )-------(6分)
)-------(6分)
令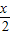 -
-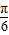 =
=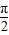 +kπ,--------(7分)
+kπ,--------(7分)
则x=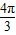 +2kπ(k∈Z),所以g(x)的对称轴方程为x=
+2kπ(k∈Z),所以g(x)的对称轴方程为x=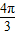 +2kπ(k∈Z),..-(8分)
+2kπ(k∈Z),..-(8分)
(3)∵x∈[0,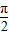 ],
],
∴2x+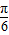 ∈[
∈[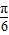 ,
,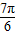 ]--------(9分)
]--------(9分)
∴当方程f(x)=2a-3有两个不等实根时,y=f(x)的图象与直线y=2a-3有两个不同的交点
∴1≤2a-3<2--------(11分)
∴2≤a< --------(12分)
--------(12分)
(法一)当x∈[0,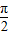 ],时,f(x1)=f(x2),
],时,f(x1)=f(x2),
所以(2x1+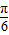 )+(2x2+
)+(2x2+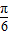 )=π,
)=π,
所以x1+x2=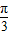 ;
;
(法二)令2x+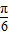 =
=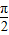 +kπ,则x=
+kπ,则x=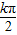 +
+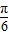 ,(k∈Z)
,(k∈Z)
所以f(x)的对称轴方程为x=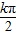 +
+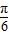 ,(k∈Z)
,(k∈Z)
又∵x∈[0,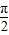 ],
],
∴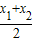 =
=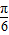 ,所以x1+x2=
,所以x1+x2=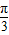 ;--(14分)
;--(14分)
点评:本题考查:由y=Asin(ωx+φ)的部分图象确定其解析式,考查函数y=Asin(ωx+φ)的图象变换及三角函数性质的综合应用,属于难题.
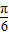 +φ)=2可求得φ;
+φ)=2可求得φ;(2)由函数y=Asin(ωx+φ)的图象变换可求得g(x)=2sin(
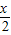 -
-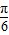 ),由正弦函数的性质即可求得g(x)的对称轴方程;
),由正弦函数的性质即可求得g(x)的对称轴方程;(3)由x∈[0,
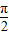 ]⇒2x+
]⇒2x+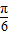 ∈[
∈[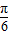 ,
,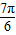 ],方程f(x)=2a-3有两个不等实根时,y=f(x)的图象与直线y=2a-3有两个不同的交点,从而可求得a的取值范围;
],方程f(x)=2a-3有两个不等实根时,y=f(x)的图象与直线y=2a-3有两个不同的交点,从而可求得a的取值范围;(法一)当x∈[0,
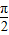 ],时,利用f(x1)=f(x2),即可求得x1+x2的值;
],时,利用f(x1)=f(x2),即可求得x1+x2的值;(法二)令2x+
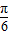 =
=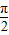 +kπ,可求得x=
+kπ,可求得x=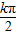 +
+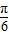 ,(k∈Z),利用f(x)的对称轴方程为x=
,(k∈Z),利用f(x)的对称轴方程为x=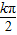 +
+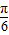 即可求得x1+x2的值.
即可求得x1+x2的值.解答:解:(1)由图知,A=2.--------(1分)
T=π,ω=
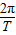 =
=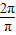 =2-----(2分)
=2-----(2分)由2sin(2×
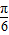 +φ)=2,即sin(
+φ)=2,即sin(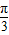 +φ)=1,故
+φ)=1,故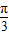 +φ=
+φ=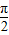 +2kπ,k∈Z,
+2kπ,k∈Z,所以φ=
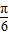 +2kπ,k∈Z,
+2kπ,k∈Z,又φ∈(0,
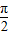 ),所以φ=
),所以φ=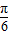 ---(3分)
---(3分)故f(x)=2sin(2x+
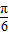 )-------(4分)
)-------(4分)(2)将f(x)的图象向右平移
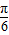 个单位后,得到f(x-
个单位后,得到f(x-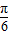 )的图象,再将所得图象横坐标伸长到原来的4倍,
)的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到f(
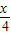 -
-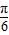 )的图象,
)的图象,所以g(x)=f(
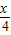 -
-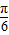 )=2sin[2(
)=2sin[2(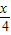 -
-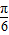 )+
)+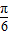 )]=2sin(
)]=2sin(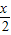 -
-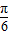 )-------(6分)
)-------(6分)令
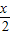 -
-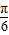 =
=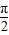 +kπ,--------(7分)
+kπ,--------(7分)则x=
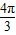 +2kπ(k∈Z),所以g(x)的对称轴方程为x=
+2kπ(k∈Z),所以g(x)的对称轴方程为x=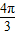 +2kπ(k∈Z),..-(8分)
+2kπ(k∈Z),..-(8分)(3)∵x∈[0,
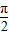 ],
],∴2x+
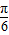 ∈[
∈[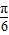 ,
,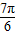 ]--------(9分)
]--------(9分)∴当方程f(x)=2a-3有两个不等实根时,y=f(x)的图象与直线y=2a-3有两个不同的交点
∴1≤2a-3<2--------(11分)
∴2≤a<
 --------(12分)
--------(12分)(法一)当x∈[0,
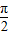 ],时,f(x1)=f(x2),
],时,f(x1)=f(x2),所以(2x1+
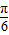 )+(2x2+
)+(2x2+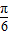 )=π,
)=π,所以x1+x2=
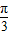 ;
;(法二)令2x+
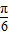 =
=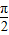 +kπ,则x=
+kπ,则x=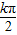 +
+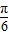 ,(k∈Z)
,(k∈Z)所以f(x)的对称轴方程为x=
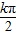 +
+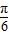 ,(k∈Z)
,(k∈Z)又∵x∈[0,
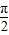 ],
],∴
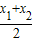 =
=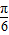 ,所以x1+x2=
,所以x1+x2=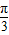 ;--(14分)
;--(14分)点评:本题考查:由y=Asin(ωx+φ)的部分图象确定其解析式,考查函数y=Asin(ωx+φ)的图象变换及三角函数性质的综合应用,属于难题.

练习册系列答案
相关题目