题目内容
(本小题12分)椭圆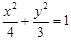 的左、右焦点分别为
的左、右焦点分别为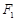 、
、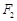 ,直线
,直线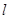 经过点
经过点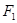 与椭圆交于
与椭圆交于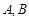 两点。
两点。
(1)求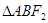 的周长;
的周长;
(2)若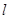 的倾斜角为
的倾斜角为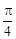 ,求
,求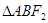 的面积。
的面积。
【答案】
(1)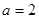 ,
, 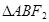 的周长为
的周长为 。
。
(2)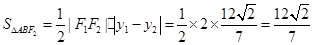 。
。
【解析】本题考查三角形周长的求法和三角形面积的计算,解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用椭圆的性质,注意椭圆定义、韦达定理在解题中的合理运用.
(1)由椭圆的定义,得AF1+AF2=2a,BF1+BF2=2a,又AF1+BF1=AB,所以,△ABF2的周长=AB+AF2+BF2=4a.再由a2=4,能导出△ABF2的周长.
(2)由F1(-1,0),AB的倾斜角为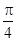 ,知直线AB的方程为y=x+1.由
,知直线AB的方程为y=x+1.由
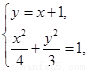
|
|
消去x,得7y2-6y-9=0,设A(x1,y1),B(x2,y2),借助韦达定理能够求出△ABF2的面积.
解:(1)由椭圆的定义,得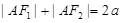 ,
,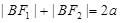 ,
----------2分
,
----------2分
又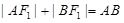 ,所以
,所以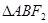 的周长为
的周长为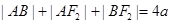 。--------4分
。--------4分
又因为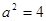 ,所以
,所以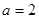 ,故
,故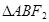 的周长为
的周长为 。-----------5分
。-----------5分
(2)由条件,得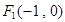 ,因为
,因为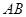 的倾斜角为
的倾斜角为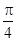 ,所以
,所以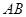 斜率为
斜率为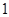 ,
,
故直线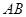 的方程为
的方程为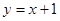 。-----------------6分
。-----------------6分
由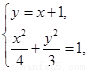 消去
消去 ,得
,得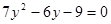 , ------------------8分
, ------------------8分
设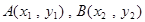 ,解得
,解得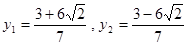 ,
-------------10分
,
-------------10分
所以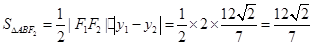 。------------------12分
。------------------12分

练习册系列答案
相关题目
 的左、右焦点,点P(-1,
的左、右焦点,点P(-1,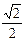 )在椭圆上,线段PF2与
)在椭圆上,线段PF2与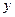 轴的交点
轴的交点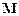 满足
满足 .(1)求椭圆的标准方程;
.(1)求椭圆的标准方程; 轴重合的直线
轴重合的直线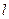 ,
,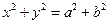 相交于A、B.并与椭圆相交于C、D.当
相交于A、B.并与椭圆相交于C、D.当 ,且
,且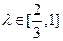 时,求△F2CD的面积S的取值范围.
时,求△F2CD的面积S的取值范围.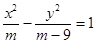 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线 的离心率
的离心率 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。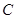 :
: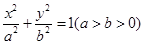 的两个焦点为
的两个焦点为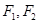 ,点
,点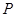 在椭圆
在椭圆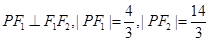 .
.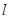 过圆
过圆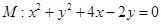 的圆心,交椭圆
的圆心,交椭圆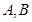 两点,且
两点,且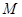 对称,求直线
对称,求直线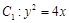 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆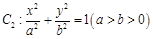 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为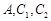 在第一象限的交点为
在第一象限的交点为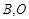 为坐标原点,且
为坐标原点,且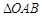 的面积为
的面积为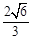
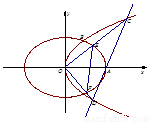
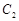 的标准方程;
的标准方程; 作直线
作直线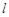 交
交 于
于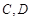 两点,射线
两点,射线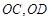 分别交
分别交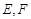 两点.
两点.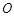 点在以
点在以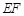 为直径的圆的内部;
为直径的圆的内部;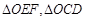 的面积分别为
的面积分别为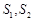 ,问是否存在直线
,问是否存在直线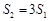 ?请说明理由.
?请说明理由.