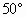题目内容
若异面直线a，b所成的角为60°，AB是公垂线，E，F分别是异面直线a，b上到A，B距离为2和1的两点，当|EF|=3时，线段AB的长为多少？分析：分析：由空间向量构造“回路向量”
+
+
+
=0，考虑到
与
，
与
，
与
的夹角较为明显，可将其变形为
=
+
+
，两边平方即可解得|
|．
| EA |
| AB |
| BF |
| FE |
| EA |
| AB |
| EA |
| BF |
| AB |
| BF |
| EF |
| EA |
| AB |
| BF |
| AB |
解答：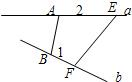
解：如图，由
+
+
+
=0，，得
2=|EA|2+
2+ |
|2+2|
|•|
|•θ
①当θ=60°时，有9=4+|
|2+1+2•2•
，得|
| =
；
②当θ=120°时，有9=4+，得|
| =
．
∴线段AB的长为
或
．
解：如图，由| EA |
| AB |
| BF |
| FE |
| |EF| |
| |AB| |
| BF |
| EA |
| BF |
①当θ=60°时，有9=4+|
| AB |
| 1 |
| 2 |
| AB |
| 2 |
②当θ=120°时，有9=4+，得|
| AB |
| 6 |
∴线段AB的长为
| 2 |
| 6 |
点评：本题考虑到若用前两种方法都难以奏效，于是选用了“回路法”，更方便了“异面直线a，b所成的角为60°”的讨论与运用，使得解题快捷无比．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
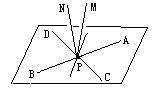
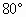，则过空间任一点P可作________条不同的直线与a，b所成角都是
，且直线c⊥a，则异面直线b，c所成角的范围是________．