题目内容
在平面直角坐标系中,已知曲线C上任意一点P到两个定点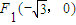 和
和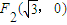 的距离之和为4.
的距离之和为4.(1)求曲线C的方程;
(2)设过(0,-2)的直线l与曲线C交于A、B两点,以线段AB为直径作圆.试问:该圆能否经过坐标原点?若能,请写出此时直线l的方程,并证明你的结论;若不是,请说明理由.
【答案】分析:(1)利用椭圆的定义即可求出;
(2)先假设符合条件的直线l存在,一方面可利用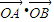 =0;另一方面把直线的方程与椭圆的方程联立,在△>0的条件下可利用根与系数的关系得到关系式,进而即可得出答案.
=0;另一方面把直线的方程与椭圆的方程联立,在△>0的条件下可利用根与系数的关系得到关系式,进而即可得出答案.
解答:解:(1)根据椭圆的定义,可知动点P的轨迹为椭圆,
其中a=2,c=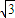 ,则
,则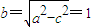 .
.
所以动点P的轨迹方程为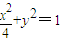 .
.
(2)当直线l的斜率不存在时,不满足题意.
当直线l的斜率存在时,设直线l的方程为y=kx-2,设A(x1,y1),B(x2,y2),
若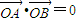 ,则x1x2+y1y2=0.
,则x1x2+y1y2=0.
∵y1=kx1-2,y2=kx2-2,∴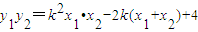 .
.
∴(1+k2)x1x2-2k(x1+x2)+4=0.…①
由方程组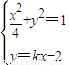 得(1+4k2)x2-16kx+12=0.
得(1+4k2)x2-16kx+12=0.
∵△=162k2-4×12×(1+4k2)>0,∴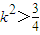 …②
…②
则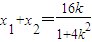 ,
,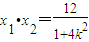 ,代入①,得
,代入①,得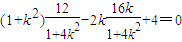 .即k2=4,解得k=2或k=-2,满足②式.
.即k2=4,解得k=2或k=-2,满足②式.
因此存在直线l,其方程为y=2x-2或y=-2x-2.
点评:熟练掌握圆锥曲线的定义与性质、两条垂直的充要条件、直线方程与圆锥曲线方程相交问题的处理方法是解题的关键.
(2)先假设符合条件的直线l存在,一方面可利用
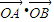 =0;另一方面把直线的方程与椭圆的方程联立,在△>0的条件下可利用根与系数的关系得到关系式,进而即可得出答案.
=0;另一方面把直线的方程与椭圆的方程联立,在△>0的条件下可利用根与系数的关系得到关系式,进而即可得出答案.解答:解:(1)根据椭圆的定义,可知动点P的轨迹为椭圆,
其中a=2,c=
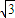 ,则
,则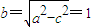 .
.所以动点P的轨迹方程为
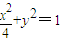 .
.(2)当直线l的斜率不存在时,不满足题意.
当直线l的斜率存在时,设直线l的方程为y=kx-2,设A(x1,y1),B(x2,y2),
若
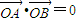 ,则x1x2+y1y2=0.
,则x1x2+y1y2=0.∵y1=kx1-2,y2=kx2-2,∴
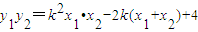 .
.∴(1+k2)x1x2-2k(x1+x2)+4=0.…①
由方程组
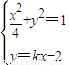 得(1+4k2)x2-16kx+12=0.
得(1+4k2)x2-16kx+12=0.∵△=162k2-4×12×(1+4k2)>0,∴
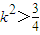 …②
…②则
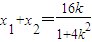 ,
,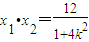 ,代入①,得
,代入①,得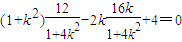 .即k2=4,解得k=2或k=-2,满足②式.
.即k2=4,解得k=2或k=-2,满足②式.因此存在直线l,其方程为y=2x-2或y=-2x-2.
点评:熟练掌握圆锥曲线的定义与性质、两条垂直的充要条件、直线方程与圆锥曲线方程相交问题的处理方法是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目