题目内容
对某校高一年级学生参加社区服务次数统计,随机抽取了 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:

(1)求出表中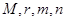 的值;
的值;
(2)在所取样本中,从参加社区服务的次数不少于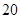 次的学生中任选
次的学生中任选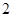 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间 内的概率.
内的概率.
 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
(1)求出表中
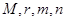 的值;
的值;(2)在所取样本中,从参加社区服务的次数不少于
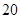 次的学生中任选
次的学生中任选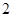 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间 内的概率.
内的概率.(1)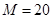 ,
,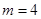 ,
,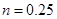 ,
,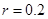 ;(2)
;(2)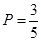 .
.
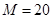 ,
,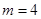 ,
,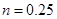 ,
,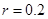 ;(2)
;(2)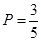 .
.试题分析:本题考查频率分布表的读法和随机事件的概率,考查学生的分析能力和计算能力.第一问,先利用频数/样本总数=频率,利用第一组数据,先求出样本总数
 ,再利用所有频数和为
,再利用所有频数和为 ,求出
,求出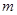 ,再利用第2组数据求
,再利用第2组数据求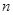 ,再利用所有频率之和为1,求
,再利用所有频率之和为1,求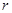 ;第二问,列出任选2名学生的所有可能结果,在其中找出符合题意的种数,求出比值即可.
;第二问,列出任选2名学生的所有可能结果,在其中找出符合题意的种数,求出比值即可.试题解析:(1)因为
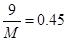 ,所以
,所以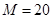 2分
2分又因为
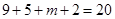 ,所以
,所以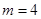 3分
3分所以
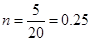 ,
,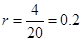 4分
4分(2)设参加社区服务的次数在
 内的学生为
内的学生为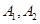 ,参加社区服务的次数在
,参加社区服务的次数在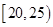 内的学生为
内的学生为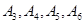 ; 5分
; 5分任选
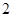 名学生的结果为:
名学生的结果为: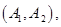
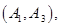
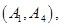
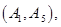
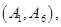
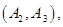
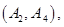
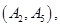
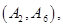
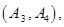
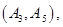
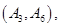
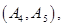
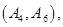
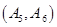 共
共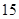 种情况 ; 8分
种情况 ; 8分其中至少一人参加社区服务次数在区间
 内的情况有
内的情况有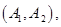
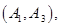
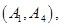
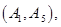
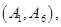
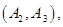
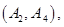
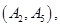
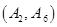 ,共
,共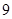 种情况 10分
种情况 10分每种情况都是等可能出现的,所以其中至少一人参加社区服务次数在区间
 内的概率为
内的概率为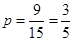 . 12分
. 12分
练习册系列答案
相关题目
 ,求随机变量
,求随机变量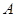 、
、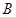 、
、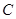 、
、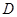 、
、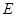 五位同学,他们的身高(单位:米)以及体重指
五位同学,他们的身高(单位:米)以及体重指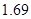
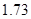
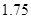

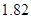





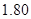 的同学中任选
的同学中任选 人,求选到的
人,求选到的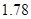 以下的概率;
以下的概率;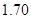 以上且体重指标都在
以上且体重指标都在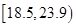 中的概率.
中的概率. ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选. ,且
,且 ,在直角坐标平面内,从所有满足这些条件的有序实数对
,在直角坐标平面内,从所有满足这些条件的有序实数对 所表示的点中任取一个,若该点落在圆
所表示的点中任取一个,若该点落在圆 内的概率为
内的概率为 ,则满足要求的
,则满足要求的 的最小值为 .
的最小值为 .


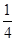
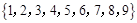 中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 .
中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 .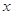 的一元二次方程
的一元二次方程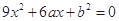 ……
……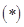 ,解决下列两个问题:
,解决下列两个问题: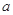 是从
是从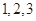 三个数中任取的一个数,
三个数中任取的一个数,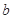 是从
是从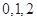 三个数中任取的一个数,求方程
三个数中任取的一个数,求方程 任取的一个数,
任取的一个数, 任取的一个数,求方程
任取的一个数,求方程