题目内容
已知点P是圆x2+y2=1上的动点,点P在y轴上的射影为Q,设满足条件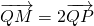 的点M的轨迹为曲线C.
的点M的轨迹为曲线C.
(1)求曲线C的方程;
(2)设过点N(1,0)且斜率为k1(k1≠0)的直线l被曲线C所截得的弦的中点为A,O为坐标原点,直线OA的斜率为k2,求k12+k22的最小值.
解:(1)设点P的坐标为(x0,y0),点M的坐标为(x,y),则点Q的坐标为(0,y0).
由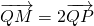 ,得x=2x0,y=y0,即
,得x=2x0,y=y0,即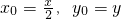 .
.
因为点P在圆x2+y2=1上,把点P代入圆x2+y2=1 可得 ,故点M的轨迹C的方程为
,故点M的轨迹C的方程为 .
.
(2)由题设知,直线l的方程为y=k1(x-1),由 ,
,
得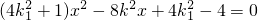 ,其中,△=64k14-4(4k12+1)(4k12-4)=16(3k12+1)>0.
,其中,△=64k14-4(4k12+1)(4k12-4)=16(3k12+1)>0.
设直线l与曲线C的两交点坐标为(x1,y1),(x2,y2),则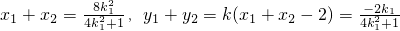 ,所以,
,所以,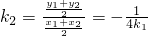 .
.
所以, ,当且仅当
,当且仅当 时取等号,故
时取等号,故 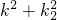 的最小值是
的最小值是 .
.
分析:(1)设点P的坐标为(x0,y0),点M的坐标为(x,y),由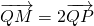 ,得x=2x0,y=y0,把点P坐标(x0,y0)代入圆x2+y2=1 消去x0,y0 可得M的轨迹C的方程.
,得x=2x0,y=y0,把点P坐标(x0,y0)代入圆x2+y2=1 消去x0,y0 可得M的轨迹C的方程.
(2)设出直线l的方程为y=k1(x-1),代入椭圆的方程,化为关于x的一元二次方程,利用根与系数,得到 ,代入要求的式子利用基本不等式求得最小值.
,代入要求的式子利用基本不等式求得最小值.
点评:本题考查求点的轨迹方程的方法,向量坐标形式的运算,一元二次方程根与系数的关系,基本不等式的应用,
得到 是解题的关键.
是解题的关键.
由
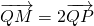 ,得x=2x0,y=y0,即
,得x=2x0,y=y0,即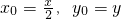 .
.因为点P在圆x2+y2=1上,把点P代入圆x2+y2=1 可得
 ,故点M的轨迹C的方程为
,故点M的轨迹C的方程为 .
.(2)由题设知,直线l的方程为y=k1(x-1),由
 ,
,得
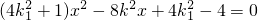 ,其中,△=64k14-4(4k12+1)(4k12-4)=16(3k12+1)>0.
,其中,△=64k14-4(4k12+1)(4k12-4)=16(3k12+1)>0.设直线l与曲线C的两交点坐标为(x1,y1),(x2,y2),则
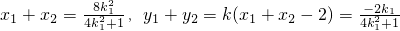 ,所以,
,所以,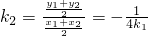 .
.所以,
 ,当且仅当
,当且仅当 时取等号,故
时取等号,故 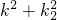 的最小值是
的最小值是 .
.分析:(1)设点P的坐标为(x0,y0),点M的坐标为(x,y),由
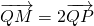 ,得x=2x0,y=y0,把点P坐标(x0,y0)代入圆x2+y2=1 消去x0,y0 可得M的轨迹C的方程.
,得x=2x0,y=y0,把点P坐标(x0,y0)代入圆x2+y2=1 消去x0,y0 可得M的轨迹C的方程.(2)设出直线l的方程为y=k1(x-1),代入椭圆的方程,化为关于x的一元二次方程,利用根与系数,得到
 ,代入要求的式子利用基本不等式求得最小值.
,代入要求的式子利用基本不等式求得最小值.点评:本题考查求点的轨迹方程的方法,向量坐标形式的运算,一元二次方程根与系数的关系,基本不等式的应用,
得到
 是解题的关键.
是解题的关键. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的点M的轨迹为曲线C.
的点M的轨迹为曲线C.