题目内容
某人要制作一个三角形，要求它的三条高的长度分别为
，则此人能( )
| A．不能作出这样的三角形 | B．作出一个锐角三角形 |
| C．作出一个直角三角形 | D．作出一个钝角三角形 |
D
解析试题分析：设三边分别为a,b,c，利用面积相等可知,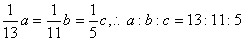
,由余弦定理得
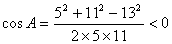，所以角A为钝角,故选D.
考点：解三角形
点评：根据三角形的三边的关系式，以及余弦定理来判定，属于基础题。
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
的内角A、B、C的对边分别是a、b、c，且a2-c2 +b2<0 ，则角C是 （ ）满足条件a=4,b=3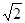
,A=45°的
ABC的个数是（ ）
| A．一个 | B．两个 | C．无数个 | D．零个 |
在
中，
，
，则的面积为（ ）
A． | B． | C． | D． |
在△ABC中，根据下列条件解三角形，则其中有两个解的是
| A．b = 10，A = 45°，B = 70° | B．a = 60，c = 48，B = 100° |
| C．a = 7，b = 5，A = 80° | D．a = 14，b = 16，A = 45° |
已知一个直角三角形的两条直角边长恰好是方程
的两根，则这个直角三角形的斜边长等于（ ）
A． | B．3 | C．6 | D．9 |
后，向右转150°，然后朝新方向走3
，结果他离出发点恰好是
，那么
的值为（ ）
△ABC中，若b=6，c=10，B=30°，则解此三角形的结果为（ ）
| A．无解 | B．有一解 | C．有两解 | D．一解或两解 |
在
中，若
，则的形状一定是( )
| A．等腰三角形 | B．直角三角形 |
| C．等腰直角三角形 | D．等边三角形 |