题目内容
已知定点 ,
, ,
, 是圆
是圆 :
: 上任意一点,点
上任意一点,点 关于点
关于点 的对称点为
的对称点为 ,线段
,线段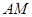 的中垂线与直线
的中垂线与直线 相交于点
相交于点 ,则点
,则点 的轨迹是
的轨迹是
| A.椭圆 | B.双曲线 | C.抛物线 | D.圆 |
B
解析试题分析:由N是圆O:x2+y2=1上任意一点,可得ON=1,且N为MF1的中点可求MF2,结合已知由垂直平分线的性质可得PM=PF1,从而可得|PF2-PF1|=|PF2-PM|=MF2=2为定值,由双曲线的定义可得点P得轨迹是以F1,F2为焦点的双曲线解:连接ON,由题意可得ON=1,且N为MF1的中点∴MF2=2,∵点F1关于点N的对称点为M,线段F1M的中垂线与直线F2M相交于点P,由垂直平分线的性质可得PM=PF1,∴|PF2-PF1|=|PF2-PM|=MF2=2<F1F2,由双曲线的定义可得点P得轨迹是以F1,F2为焦点的双曲线,故选:B
考点:双曲线的定义
点评:本题以圆为载体,考查了利用双曲线的定义判断圆锥曲线的类型的问题,解决本题的关键是由N为圆上一点可得ON=1,结合N为MF1的中点,由三角形中位线的性质可得MF2=2,还要灵活应用垂直平分线的性质得到解决本题的第二个关键点|PF2-PF1|=|PF2-PM|=MF2=2<F1F2,从而根据圆锥曲线的定义可求解,体现了转化思想的应用.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
设 ,则方程
,则方程 不能表示的曲线为( )
不能表示的曲线为( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
如果方程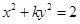 表示焦点在y轴上的椭圆,则实数k的取值范围是( )
表示焦点在y轴上的椭圆,则实数k的取值范围是( )
| A.(0,+∞) | B.(0,2) | C.(1,+∞) | D.(0,1) |
 , 一个焦点为
, 一个焦点为 的椭圆,截直线
的椭圆,截直线 所得弦中点的横坐标为
所得弦中点的横坐标为 ,则该椭圆方程是( )
,则该椭圆方程是( )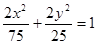
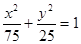
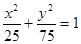

 是双曲线
是双曲线 的左焦点,
的左焦点, 是双曲线的右顶点,过点
是双曲线的右顶点,过点 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若
两点,若 是锐角三角形,则该双曲线的离心率
是锐角三角形,则该双曲线的离心率 的取值范围为( )
的取值范围为( )



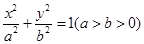 的左、右焦点分别为F1、F2,P是椭圆上的一点,
的左、右焦点分别为F1、F2,P是椭圆上的一点, ,且
,且 ,垂足为
,垂足为 ,若四边形
,若四边形 为平行四边形,则椭圆的离心率的取值范围是( )
为平行四边形,则椭圆的离心率的取值范围是( )



 和
和 (其中
(其中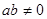 ,
, ),它们所表示的曲线可能是( )
),它们所表示的曲线可能是( )
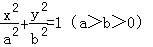 上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )


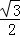
 的右焦点为
的右焦点为 ,离心率等于
,离心率等于 ,在双曲线
,在双曲线


