题目内容
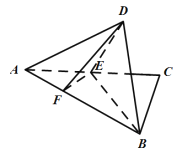
【题目】四棱台被过点![]() 的平面截去一部分后得到如图所示的几何体,其下底面四边形
的平面截去一部分后得到如图所示的几何体,其下底面四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 与底面
与底面![]() 所成角的正切值为2,求二面角
所成角的正切值为2,求二面角![]() 的余弦值.
的余弦值.

【答案】(I)详见解析;(II)![]() .
.
【解析】试题分析:(Ⅰ)易证![]() ,
,![]() ,进而可得
,进而可得![]() 平面
平面![]() ,从而证得;
,从而证得;
(Ⅱ)![]() 与底面
与底面![]() 所成角为
所成角为![]() ,从而可得
,从而可得![]() ,设
,设![]() ,
,![]() 交于点
交于点![]() ,以
,以![]() 为坐标原点建立空间直角坐标系,分别求平面
为坐标原点建立空间直角坐标系,分别求平面![]() 和平面
和平面![]() 的法向量,利用法向量求解二面角即可.
的法向量,利用法向量求解二面角即可.
试题解析:
(Ⅰ)∵![]() 平面
平面![]() ,∴
,∴![]() .
.
在菱形![]() 中,
中,![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(Ⅱ)∵![]() 平面
平面![]()
∴![]() 与底面
与底面![]() 所成角为
所成角为![]() ,∴
,∴![]() ,∴
,∴![]()
设![]() ,
,![]() 交于点
交于点![]() ,以
,以![]() 为坐标原点,如图建立空间直角坐标系.
为坐标原点,如图建立空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,
同理![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
∴ 则
则![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
 则
则![]() ,
,
设二面角![]() 为
为![]() ,
, .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】直角三角形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一个动点,且
上一个动点,且![]() ,如图所示,沿
,如图所示,沿![]() 将
将![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
(1)当![]() 时,证明:
时,证明:![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【题目】【2018四川南充高三第二次(3月)高考适应性考试】某校开展“翻转合作学习法”教学试验,经过一年的实践后,对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试,按照大于或等于120分为“成绩优秀”,120分以下为“成绩一般”统计,得到如下的![]() 列联表:
列联表:
成绩优秀 | 成绩一般 | 合计 | |
对照班 | 20 | 90 | 110 |
翻转班 | 40 | 70 | 110 |
合计 | 60 | 160 | 220 |
(I)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关;
(II)为了交流学习方法,从这次测试数学成绩优秀的学生中,用分层抽样方法抽出6名学生,再从这6名学生中抽3名出来交流学习方法,求至少抽到1名“对照班”学生交流的概率.
附表:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |



