题目内容
已知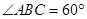 ,
,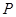 为
为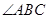 内一定点,且点
内一定点,且点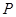 到边
到边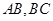 的距离分别为1,2.则
的距离分别为1,2.则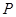 点到顶点
点到顶点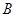 的距离为 .
的距离为 .
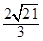
解析试题分析:设从P往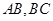 引垂线,垂足为E、F,取BP 的中点O,连接OE、OF,则OE、OF为四边形ABCP外接圆的半径,不妨设为r。因为
引垂线,垂足为E、F,取BP 的中点O,连接OE、OF,则OE、OF为四边形ABCP外接圆的半径,不妨设为r。因为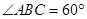 ,所以
,所以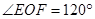 ,
,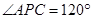 ,在
,在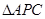 中,由余弦定理,得:
中,由余弦定理,得: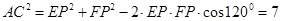 。在
。在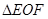 中,由余弦定理,得:
中,由余弦定理,得: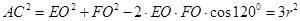 。所以
。所以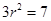 ,
,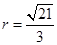 ,又
,又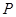 点到顶点
点到顶点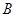 的距离为四边形ABCP外接圆的直径,即2r,所以
的距离为四边形ABCP外接圆的直径,即2r,所以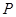 点到顶点
点到顶点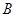 的距离为
的距离为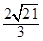 。
。
考点:余弦定理;外接圆的有关性质。
点评:此题构造出四边形ABCP的外接圆,在三角形中利用余弦定理是解题的关键,难度较大,对学生的能力要求较高。

练习册系列答案
相关题目
 ,则存在正实数
,则存在正实数 ,使得
,使得 ;③若函数
;③若函数 在点
在点 处取得极值,则实数
处取得极值,则实数 或
或 ;④函数
;④函数 有且只有一个零点.其中正确命题的序号是 .
有且只有一个零点.其中正确命题的序号是 . ,则
,则 .
.  ,当竹竿滑动到A1B1位置时,
,当竹竿滑动到A1B1位置时, ,竹竿在滑动时中点T也沿着某种轨迹运动到T1点,则T运动的路程是_________米.
,竹竿在滑动时中点T也沿着某种轨迹运动到T1点,则T运动的路程是_________米.
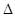 ABC中,已知
ABC中,已知 ,则
,则 ,则
,则 =
=  中,
中, ,则角
,则角 _____________。
_____________。 中,
中, 分别为角
分别为角 所对的边,若
所对的边,若 ,则
,则 .
. ,b=1,c=2,则A等于
,b=1,c=2,则A等于