题目内容
有如下列命题:①三边是连续的三个自然数,且最大角是最小角的2倍的三角形存在且唯一;②若 ,则存在正实数
,则存在正实数 ,使得
,使得 ;③若函数
;③若函数 在点
在点 处取得极值,则实数
处取得极值,则实数 或
或 ;④函数
;④函数 有且只有一个零点.其中正确命题的序号是 .
有且只有一个零点.其中正确命题的序号是 .
①④
解析试题分析:①三边是连续的三个自然数,可设为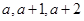 且最大角是最小角的2倍,设最小角为
且最大角是最小角的2倍,设最小角为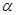 ,则最大角为
,则最大角为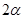 ,由正弦定理得
,由正弦定理得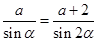 ,即
,即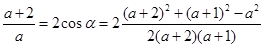 ,解得
,解得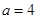 ,所以三边为
,所以三边为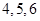 ,满足条件的三角形存在且唯一;②若
,满足条件的三角形存在且唯一;②若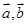 有一个为零向量,
有一个为零向量, 成立,这时不存在正实数
成立,这时不存在正实数 ,使得
,使得 ;③若函数
;③若函数 在点
在点 处取得极值,
处取得极值,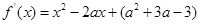 在
在 处为零,即
处为零,即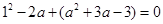 ,解得
,解得 或
或 ,但
,但 时
时 ,不是极值点;④函数
,不是极值点;④函数 的零点,即
的零点,即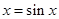 的解,即函数
的解,即函数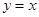 与
与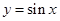 的交点,由下图可知只有一个交点,故函数
的交点,由下图可知只有一个交点,故函数 有且只有一个零点.故①④正确.
有且只有一个零点.故①④正确.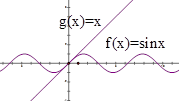
考点:1、解三角形,2、向量的数量积,3、利用导数求极值,4、正弦函数的图像.

练习册系列答案
相关题目
 中,
中, ,
, ,
, ,则
,则 .
. 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,A = 45°,B = 60°,那么△ABC的面积
,A = 45°,B = 60°,那么△ABC的面积 .
. 分别是其对边长,向量
分别是其对边长,向量 ,
, ,
, ,且
,且
 则
则 .
.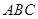 中,角
中,角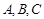 所对应的边分别为
所对应的边分别为 ,若
,若 ,则角
,则角 等于________.
等于________. 中,角
中,角 的对边分别是
的对边分别是 ,若
,若 ,
, ,则
,则 中,角
中,角 所对的边分别为
所对的边分别为 满足
满足 ,
, ,
, ,则
,则 的取值范围是 .
的取值范围是 .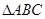 中,已知
中,已知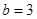 ,
,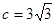 ,
,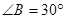 ,则
,则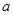 等于_____________.
等于_____________.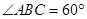 ,
,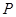 为
为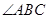 内一定点,且点
内一定点,且点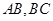 的距离分别为1,2.则
的距离分别为1,2.则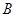 的距离为 .
的距离为 .