题目内容
函数 的定义域为
的定义域为 ,
, ,对任意
,对任意 ,
, ,则
,则
的解集为
 的定义域为
的定义域为 ,
, ,对任意
,对任意 ,
, ,则
,则
的解集为
A.( ,1) ,1) | B.( ,+ ,+ ) ) | C.( , , ) ) | D.( ,+ ,+ ) ) |
B
构建函数F(x)=f(x)-(2x+4),由f(-1)=2得出F(-1)的值,求出F(x)的导函数,根据f′(x)>2,得到F(x)在R上为增函数,根据函数的增减性即可得到F(x)大于0的解集,进而得到所求不等式的解集.
解:设F(x)=f(x)-(2x+4),
则F(-1)=f(-1)-(-2+4)=2-2=0,
又对任意x∈R,f′(x)>2,所以F′(x)=f′(x)-2>0,
即F(x)在R上单调递增,
则F(x)>0的解集为(-1,+∞),
即f(x)>2x+4的解集为(-1,+∞).
故答案为B
解:设F(x)=f(x)-(2x+4),
则F(-1)=f(-1)-(-2+4)=2-2=0,
又对任意x∈R,f′(x)>2,所以F′(x)=f′(x)-2>0,
即F(x)在R上单调递增,
则F(x)>0的解集为(-1,+∞),
即f(x)>2x+4的解集为(-1,+∞).
故答案为B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
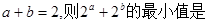 ( )
( )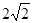
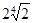
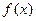 的定义域是R,对于任意实数
的定义域是R,对于任意实数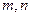 ,恒有
,恒有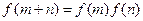 ,且当
,且当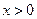 时,
时,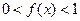 。
。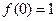 ,且当
,且当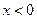 时,有
时,有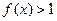 ;
;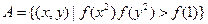 ,集合
,集合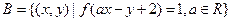 ,若A∩B=
,若A∩B=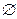 ,求a的取值范围。
,求a的取值范围。 与函数
与函数 的图象关于( )
的图象关于( ) 轴对称
轴对称 对称
对称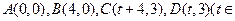 R)。记
R)。记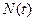 为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则
为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则 ;
; ,
, 为实数,(
为实数,( ).
). ,求函数
,求函数 的极值;
的极值; ,且函数
,且函数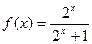 的值域为 .
的值域为 . ,若函数
,若函数 有3个零点,则实数
有3个零点,则实数 的
的 在
在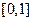 上的最大值与最小值之和为
上的最大值与最小值之和为 ,则
,则