题目内容
【题目】已知点F是抛物线C：y2＝2px（p＞0）的焦点，过点F的直线与抛物线相交于A，B两点（点A在x轴上方），与y轴的正半轴相交于点N，点Q是抛物线不同于A，B的点，若2
，则|BF|：|BA|：|BN|＝_____．
【答案】2：3：4
【解析】
点F
，设直线AB的方程为
，所以点N（
），由2
可知点A是线段NF的中点，所以点A（
），联立直线AB与抛物线的方程，消去y得到关于x的一元二次方程，由韦达定理可知，
，xB＝p，然后利用抛物线的定义逐一用含有p的式子表示出线段|BF|、|BA|和|BN|的长，即可得解．
由题可知，点F，设直线AB的方程为，
令x＝0，则y
，∴点N（），
∵2，∴点A是线段NF的中点，∴点A（），
联立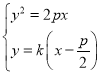
，得
，
∴，∴
，
由抛物线的定义可知，|BF|
，
|BA|
，
|BN|＝|BA|+|AN|＝|BA|+|AF|
，
∴|BF|：|BA|：|BN|
．
故答案为：2：3：4．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
